Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 218163 by hardmath last updated on 31/Mar/25

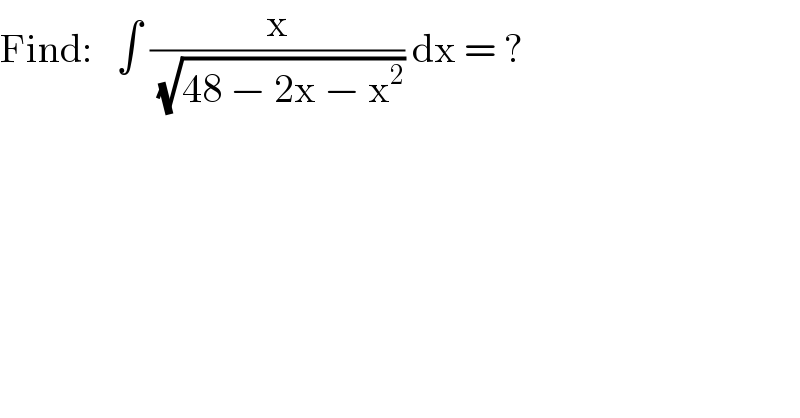
Find: ∫ (x/( (√(48 − 2x − x^2 )))) dx = ?

$$\mathrm{Find}:\:\:\:\int\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{48}\:−\:\mathrm{2x}\:−\:\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\:=\:? \\ $$

Answered by efronzo1 last updated on 31/Mar/25

I= ∫ (x/( (√(49−(x+1)^2 )))) dx x+1 = 7sin u dx = 7cos u du I = ∫ ((7sin u−1)/( 7(√(1−sin^2 u)))) . 7cos u du = ∫ (7sin u−1) du = −7cos u − u + c = −7(((√(48−2x−x^2 ))/7))−arcsin (((x+1)/7))+c = −(√(48−2x−x^2 ))−arcsin (((x+1)/7))+c

$$\:\mathrm{I}=\:\int\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{49}−\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }}\:\mathrm{dx} \\ $$$$\:\mathrm{x}+\mathrm{1}\:=\:\mathrm{7sin}\:\:\mathrm{u}\: \\ $$$$\:\mathrm{dx}\:=\:\mathrm{7cos}\:\mathrm{u}\:\mathrm{du} \\ $$$$\:\mathrm{I}\:=\:\int\:\frac{\mathrm{7sin}\:\mathrm{u}−\mathrm{1}}{\:\mathrm{7}\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{u}}}\:.\:\mathrm{7cos}\:\mathrm{u}\:\mathrm{du} \\ $$$$\:\:\:=\:\int\:\left(\mathrm{7sin}\:\mathrm{u}−\mathrm{1}\right)\:\mathrm{du} \\ $$$$\:\:=\:−\mathrm{7cos}\:\mathrm{u}\:−\:\mathrm{u}\:+\:\mathrm{c} \\ $$$$\:=\:−\mathrm{7}\left(\frac{\sqrt{\mathrm{48}−\mathrm{2x}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{7}}\right)−\mathrm{arcsin}\:\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{7}}\right)+\mathrm{c} \\ $$$$\:=\:−\sqrt{\mathrm{48}−\mathrm{2x}−\mathrm{x}^{\mathrm{2}} }−\mathrm{arcsin}\:\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{7}}\right)+\mathrm{c}\: \\ $$

Commented by hardmath last updated on 31/Mar/25

thank you dear ser

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{ser} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com