Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 217326 by Rasheed.Sindhi last updated on 10/Mar/25

Find three consecutive integers such that the sum of their squares is 50.

$${Find}\:{three}\:{consecutive}\:{integers}\: \\ $$$${such}\:{that}\:{the}\:{sum}\:{of}\:{their}\:{squares} \\ $$$$\:{is}\:\mathrm{50}. \\ $$

Answered by Hanuda354 last updated on 10/Mar/25

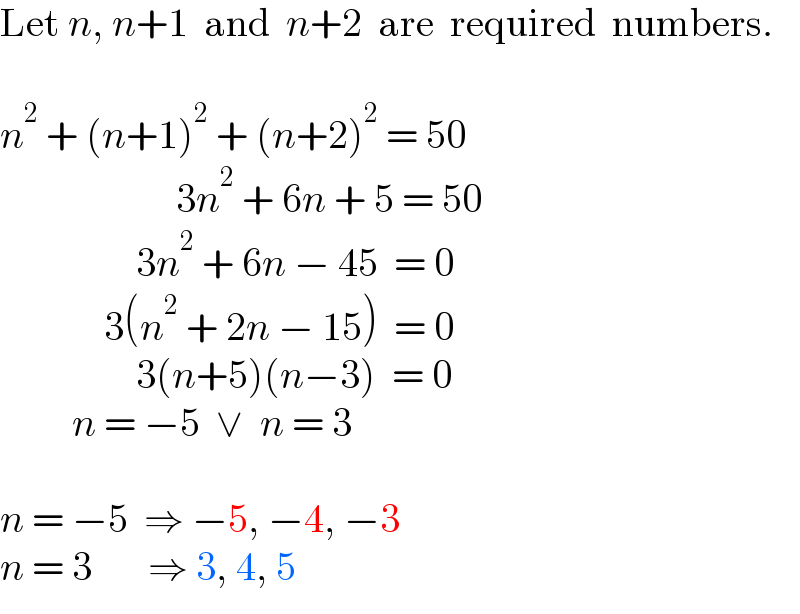
Let n, n+1 and n+2 are required numbers. n^2 + (n+1)^2 + (n+2)^2 = 50 3n^2 + 6n + 5 = 50 3n^2 + 6n − 45 = 0 3(n^2 + 2n − 15) = 0 3(n+5)(n−3) = 0 n = −5 ∨ n = 3 n = −5 ⇒ −5, −4, −3 n = 3 ⇒ 3, 4, 5

$$\mathrm{Let}\:{n},\:{n}+\mathrm{1}\:\:\mathrm{and}\:\:{n}+\mathrm{2}\:\:\mathrm{are}\:\:\mathrm{required}\:\:\mathrm{numbers}. \\ $$$$ \\ $$$${n}^{\mathrm{2}} \:+\:\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:+\:\left({n}+\mathrm{2}\right)^{\mathrm{2}} \:=\:\mathrm{50} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}{n}^{\mathrm{2}} \:+\:\mathrm{6}{n}\:+\:\mathrm{5}\:=\:\mathrm{50} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}{n}^{\mathrm{2}} \:+\:\mathrm{6}{n}\:−\:\mathrm{45}\:\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\left({n}^{\mathrm{2}} \:+\:\mathrm{2}{n}\:−\:\mathrm{15}\right)\:\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\left({n}+\mathrm{5}\right)\left({n}−\mathrm{3}\right)\:\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:{n}\:=\:−\mathrm{5}\:\:\vee\:\:{n}\:=\:\mathrm{3} \\ $$$$ \\ $$$${n}\:=\:−\mathrm{5}\:\:\Rightarrow\:−\mathrm{5},\:−\mathrm{4},\:−\mathrm{3} \\ $$$${n}\:=\:\mathrm{3}\:\:\:\:\:\:\:\Rightarrow\:\mathrm{3},\:\mathrm{4},\:\mathrm{5} \\ $$

Commented by Rasheed.Sindhi last updated on 10/Mar/25

ThanX sir!

$$\mathcal{T}{han}\mathcal{X}\:{sir}! \\ $$

Answered by Rasheed.Sindhi last updated on 10/Mar/25

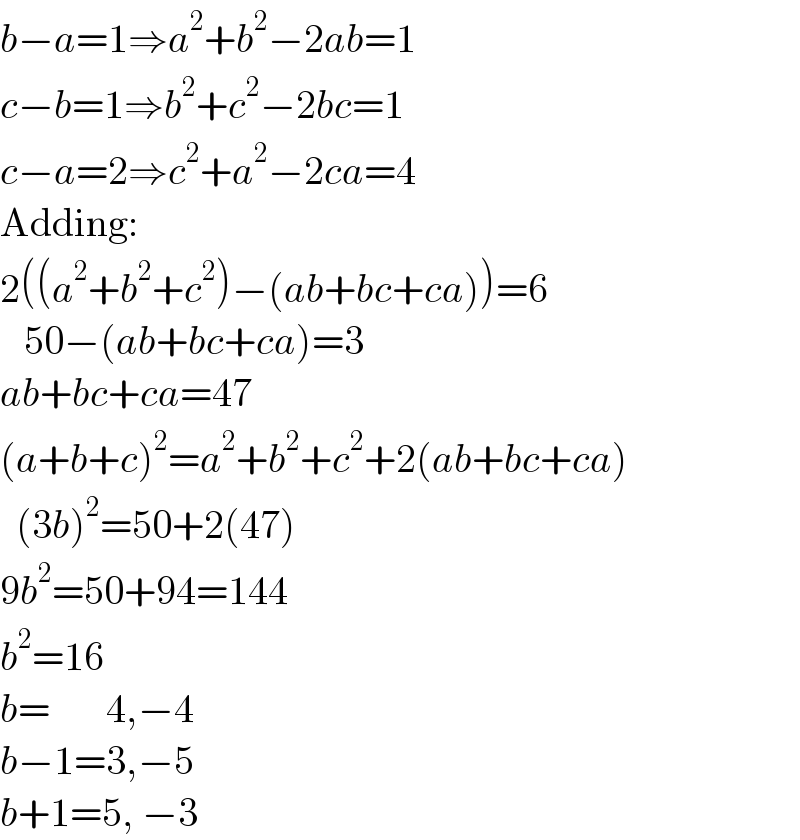
b−a=1⇒a^2 +b^2 −2ab=1 c−b=1⇒b^2 +c^2 −2bc=1 c−a=2⇒c^2 +a^2 −2ca=4 Adding: 2((a^2 +b^2 +c^2 )−(ab+bc+ca))=6 50−(ab+bc+ca)=3 ab+bc+ca=47 (a+b+c)^2 =a^2 +b^2 +c^2 +2(ab+bc+ca) (3b)^2 =50+2(47) 9b^2 =50+94=144 b^2 =16 b= 4,−4 b−1=3,−5 b+1=5, −3

$${b}−{a}=\mathrm{1}\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}=\mathrm{1} \\ $$$${c}−{b}=\mathrm{1}\Rightarrow{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}=\mathrm{1} \\ $$$${c}−{a}=\mathrm{2}\Rightarrow{c}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{ca}=\mathrm{4} \\ $$$$\mathrm{Adding}: \\ $$$$\mathrm{2}\left(\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−\left({ab}+{bc}+{ca}\right)\right)=\mathrm{6} \\ $$$$\:\:\:\mathrm{50}−\left({ab}+{bc}+{ca}\right)=\mathrm{3} \\ $$$${ab}+{bc}+{ca}=\mathrm{47} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$$\:\:\left(\mathrm{3}{b}\right)^{\mathrm{2}} =\mathrm{50}+\mathrm{2}\left(\mathrm{47}\right) \\ $$$$\mathrm{9}{b}^{\mathrm{2}} =\mathrm{50}+\mathrm{94}=\mathrm{144} \\ $$$${b}^{\mathrm{2}} =\mathrm{16} \\ $$$${b}=\:\:\:\:\:\:\:\mathrm{4},−\mathrm{4} \\ $$$${b}−\mathrm{1}=\mathrm{3},−\mathrm{5} \\ $$$${b}+\mathrm{1}=\mathrm{5},\:−\mathrm{3} \\ $$

Answered by mr W last updated on 10/Mar/25

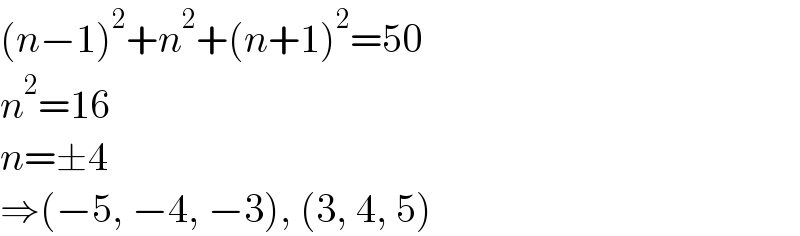
(n−1)^2 +n^2 +(n+1)^2 =50 n^2 =16 n=±4 ⇒(−5, −4, −3), (3, 4, 5)

$$\left({n}−\mathrm{1}\right)^{\mathrm{2}} +{n}^{\mathrm{2}} +\left({n}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{50} \\ $$$${n}^{\mathrm{2}} =\mathrm{16} \\ $$$${n}=\pm\mathrm{4} \\ $$$$\Rightarrow\left(−\mathrm{5},\:−\mathrm{4},\:−\mathrm{3}\right),\:\left(\mathrm{3},\:\mathrm{4},\:\mathrm{5}\right) \\ $$

Commented by Rasheed.Sindhi last updated on 10/Mar/25

Thanks sir!

$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\mathrm{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com