Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 217321 by ArshadS last updated on 10/Mar/25

Find three consecutive integers such that the product of the first two is 16 more than twice the third integer. Provide all possible solutions.

$$\mathrm{Find}\:\mathrm{three}\:\mathrm{consecutive}\:\mathrm{integers}\:\mathrm{such}\:\mathrm{that}\:\mathrm{the}\:\mathrm{product}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{first}\:\mathrm{two}\:\mathrm{is}\:\mathrm{16}\:\mathrm{more}\:\mathrm{than}\:\mathrm{twice}\:\mathrm{the}\:\mathrm{third}\:\mathrm{integer}.\:\mathrm{Provide}\:\mathrm{all}\: \\ $$$$\mathrm{possible}\:\mathrm{solutions}. \\ $$

Answered by Rasheed.Sindhi last updated on 10/Mar/25

let x−1,x,x+1 are required numbers According to given: x(x−1)=2(x+1)+16 x^2 −x=2x+2+16 x^2 −3x−18=0 x^2 −6x+3x−18=0 x(x−6)+3(x−6)=0 (x−6)(x+3)=0 x=6,−3 x=6 : 6−1^(x−1) ,6^(x) ,6+1^(x+1) 5,6,7 x=−3 : −3−1^(x−1) ,−3^(x) ,−3+1^(x+1) −4,−3,−2

$${let}\:{x}−\mathrm{1},{x},{x}+\mathrm{1}\:{are}\:{required}\:{numbers} \\ $$$${According}\:{to}\:{given}: \\ $$$${x}\left({x}−\mathrm{1}\right)=\mathrm{2}\left({x}+\mathrm{1}\right)+\mathrm{16} \\ $$$${x}^{\mathrm{2}} −{x}=\mathrm{2}{x}+\mathrm{2}+\mathrm{16} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{18}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{3}{x}−\mathrm{18}=\mathrm{0} \\ $$$${x}\left({x}−\mathrm{6}\right)+\mathrm{3}\left({x}−\mathrm{6}\right)=\mathrm{0} \\ $$$$\left({x}−\mathrm{6}\right)\left({x}+\mathrm{3}\right)=\mathrm{0} \\ $$$${x}=\mathrm{6},−\mathrm{3} \\ $$$${x}=\mathrm{6}\:: \\ $$$$\:\:\:\:\overset{{x}−\mathrm{1}} {\mathrm{6}−\mathrm{1}},\overset{{x}} {\mathrm{6}},\overset{{x}+\mathrm{1}} {\mathrm{6}+\mathrm{1}}\: \\ $$$$\:\:\:\:\mathrm{5},\mathrm{6},\mathrm{7} \\ $$$${x}=−\mathrm{3}\:: \\ $$$$\overset{{x}−\mathrm{1}} {−\mathrm{3}−\mathrm{1}},\overset{{x}} {−\mathrm{3}},\overset{{x}+\mathrm{1}} {−\mathrm{3}+\mathrm{1}} \\ $$$$\:\:\:−\mathrm{4},−\mathrm{3},−\mathrm{2} \\ $$

Commented by ArshadS last updated on 10/Mar/25

Right!

$${Right}! \\ $$

Answered by mehdee7396 last updated on 10/Mar/25

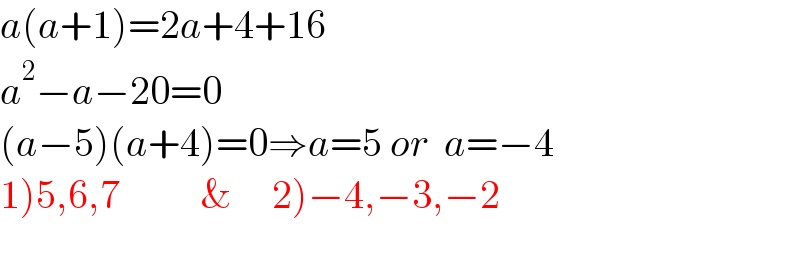
a(a+1)=2a+4+16 a^2 −a−20=0 (a−5)(a+4)=0⇒a=5 or a=−4 1)5,6,7 & 2)−4,−3,−2

$${a}\left({a}+\mathrm{1}\right)=\mathrm{2}{a}+\mathrm{4}+\mathrm{16} \\ $$$${a}^{\mathrm{2}} −{a}−\mathrm{20}=\mathrm{0} \\ $$$$\left({a}−\mathrm{5}\right)\left({a}+\mathrm{4}\right)=\mathrm{0}\Rightarrow{a}=\mathrm{5}\:{or}\:\:{a}=−\mathrm{4} \\ $$$$\left.\mathrm{1}\left.\right)\mathrm{5},\mathrm{6},\mathrm{7}\:\:\:\:\:\:\:\:\:\:\&\:\:\:\:\:\mathrm{2}\right)−\mathrm{4},−\mathrm{3},−\mathrm{2} \\ $$$$ \\ $$

Commented by ArshadS last updated on 10/Mar/25

Ok, thanks sir!

$${Ok},\:{thanks}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com