Question Number 214509 by depressiveshrek last updated on 10/Dec/24

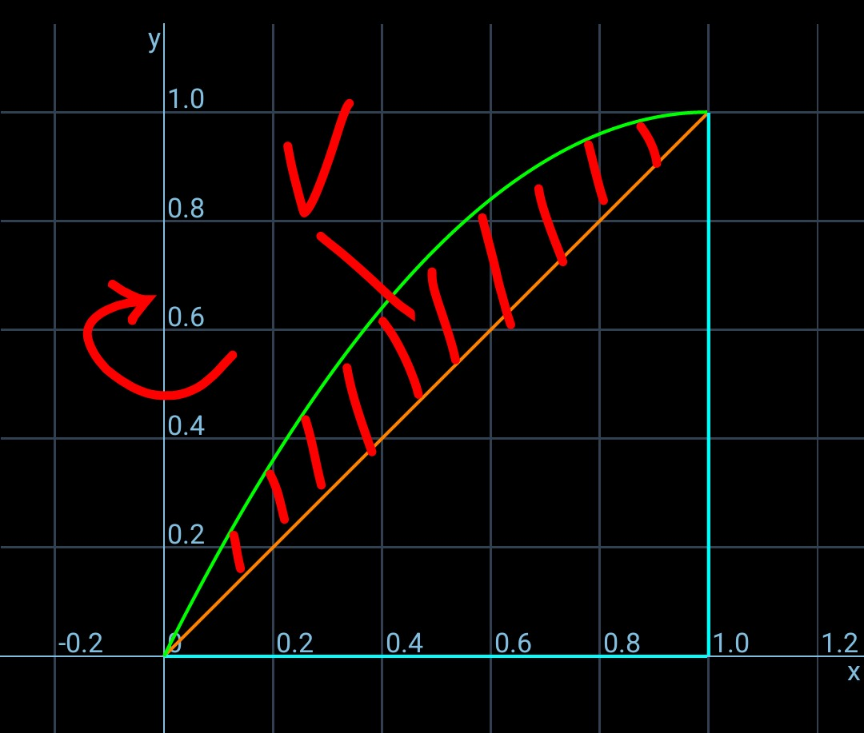
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{volume}\:\mathrm{of}\:\mathrm{the}\:\mathrm{solid}\:\mathrm{of}\:\mathrm{revolution} \\ $$$$\mathrm{generated}\:\mathrm{by}\:\mathrm{rotating}\:\mathrm{the}\:\mathrm{area}\:\mathrm{bounded} \\ $$$$\mathrm{by}\:{y}={x}\left(\mathrm{2}−{x}\right)\:\mathrm{and}\:{y}={x}\:\mathrm{about}\:\mathrm{the}\:\mathrm{y}−\mathrm{axis}. \\ $$
Commented by mr W last updated on 11/Dec/24
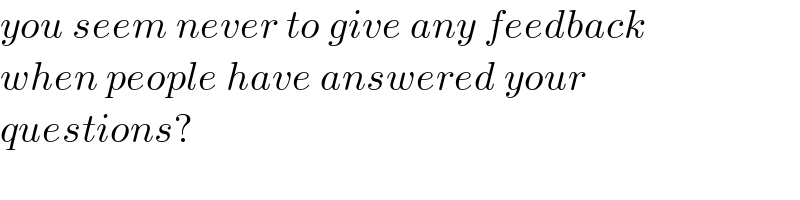
$${you}\:{seem}\:{never}\:{to}\:{give}\:{any}\:{feedback} \\ $$$${when}\:{people}\:{have}\:{answered}\:{your} \\ $$$${questions}? \\ $$
Commented by depressiveshrek last updated on 11/Dec/24
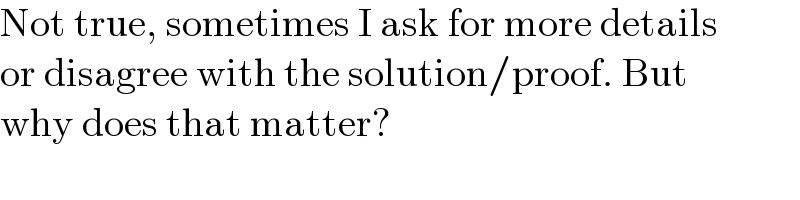
$$\mathrm{Not}\:\mathrm{true},\:\mathrm{sometimes}\:\mathrm{I}\:\mathrm{ask}\:\mathrm{for}\:\mathrm{more}\:\mathrm{details} \\ $$$$\mathrm{or}\:\mathrm{disagree}\:\mathrm{with}\:\mathrm{the}\:\mathrm{solution}/\mathrm{proof}.\:\mathrm{But} \\ $$$$\mathrm{why}\:\mathrm{does}\:\mathrm{that}\:\mathrm{matter}? \\ $$
Commented by mr W last updated on 11/Dec/24

$${actually}\:{it}\:{doesn}'{t}\:{matter}.\:{i}\:{just} \\ $$$${thought},\:{normally}\:{when}\:{somebody} \\ $$$${has}\:{recieved}\:{the}\:{help}\:{he}\:{had}\:{wished}, \\ $$$${he}'{ll}\:{show}\:{some}\:{reaction},\:{normally}. \\ $$
Commented by depressiveshrek last updated on 11/Dec/24

$$\mathrm{Okay}\:\mathrm{then}\:\mathrm{I}\:\mathrm{will}\:\mathrm{start}\:\mathrm{to}\:\mathrm{give}\:\mathrm{feedback} \\ $$$$\mathrm{from}\:\mathrm{now}\:\mathrm{on}\:\mathrm{more}\:\mathrm{frequently}. \\ $$
Answered by mr W last updated on 11/Dec/24
![x=y x^2 −2x+1=1−y ⇒x=1−(√(1−y)) 1−(√(1−y))=y ⇒y=0, 1 V=∫_0 ^1 π[y^2 −(1−(√(1−y)))^2 ]dy =∫_0 ^1 π(y^2 +y−2+2(√(1−y)))dy =π[(y^3 /3)+(y^2 /2)−2y−(4/3)(1−y)^(3/2) ]_0 ^1 =π((1/3)+(1/2)−2+(4/3)) =(π/6) ✓](Q214531.png)
$${x}={y} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}=\mathrm{1}−{y}\:\Rightarrow{x}=\mathrm{1}−\sqrt{\mathrm{1}−{y}} \\ $$$$\mathrm{1}−\sqrt{\mathrm{1}−{y}}={y}\:\Rightarrow{y}=\mathrm{0},\:\mathrm{1} \\ $$$${V}=\int_{\mathrm{0}} ^{\mathrm{1}} \pi\left[{y}^{\mathrm{2}} −\left(\mathrm{1}−\sqrt{\mathrm{1}−{y}}\right)^{\mathrm{2}} \right]{dy} \\ $$$$\:=\int_{\mathrm{0}} ^{\mathrm{1}} \pi\left({y}^{\mathrm{2}} +{y}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{1}−{y}}\right){dy} \\ $$$$\:=\pi\left[\frac{{y}^{\mathrm{3}} }{\mathrm{3}}+\frac{{y}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{y}−\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{1}−{y}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\pi\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}+\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$$$=\frac{\pi}{\mathrm{6}}\:\checkmark \\ $$
Commented by depressiveshrek last updated on 11/Dec/24

$$\mathrm{Thank}\:\mathrm{you} \\ $$
Commented by mr W last updated on 11/Dec/24
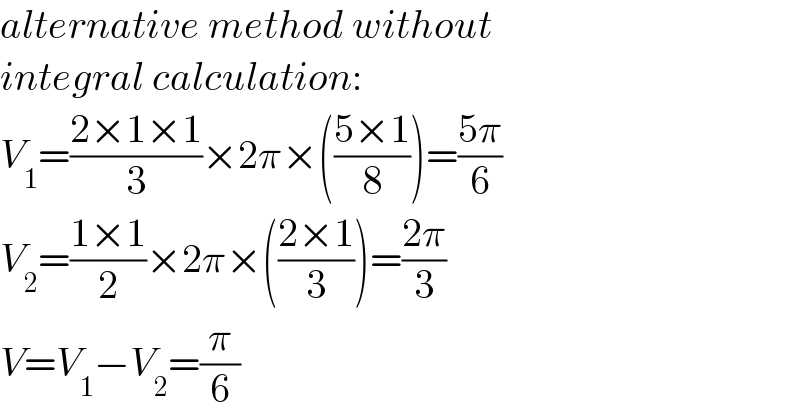
$${alternative}\:{method}\:{without} \\ $$$${integral}\:{calculation}: \\ $$$${V}_{\mathrm{1}} =\frac{\mathrm{2}×\mathrm{1}×\mathrm{1}}{\mathrm{3}}×\mathrm{2}\pi×\left(\frac{\mathrm{5}×\mathrm{1}}{\mathrm{8}}\right)=\frac{\mathrm{5}\pi}{\mathrm{6}} \\ $$$${V}_{\mathrm{2}} =\frac{\mathrm{1}×\mathrm{1}}{\mathrm{2}}×\mathrm{2}\pi×\left(\frac{\mathrm{2}×\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$${V}={V}_{\mathrm{1}} −{V}_{\mathrm{2}} =\frac{\pi}{\mathrm{6}} \\ $$
Commented by mr W last updated on 11/Dec/24
Commented by mr W last updated on 11/Dec/24