Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 213841 by mnjuly1970 last updated on 18/Nov/24

Find the vertical asymptots of , f(x)= tan((( π)/(2x + 2)) ) in [ 0 , 4 ] −−−−−−−−−−−−−

$$ \\ $$$$\:\:{Find}\:{the}\:{vertical}\:{asymptots} \\ $$$$\: \\ $$$$\:\:{of}\:\:,\:\:\:{f}\left({x}\right)=\:\mathrm{tan}\left(\frac{\:\pi}{\mathrm{2}{x}\:+\:\mathrm{2}}\:\right)\:\:{in}\: \\ $$$$\: \\ $$$$\:\:\:\:\:\left[\:\mathrm{0}\:\:,\:\:\:\mathrm{4}\:\right] \\ $$$$\:−−−−−−−−−−−−− \\ $$$$ \\ $$

Answered by efronzo1 last updated on 18/Nov/24

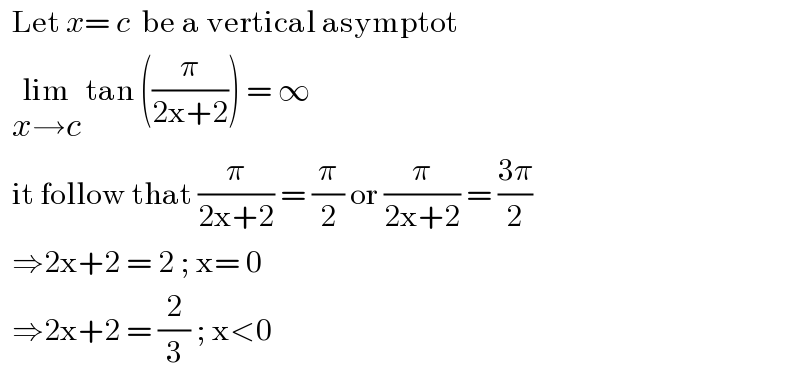
Let x= c be a vertical asymptot lim_(x→c) tan ((π/(2x+2))) = ∞ it follow that (π/(2x+2)) = (π/2) or (π/(2x+2)) = ((3π)/2) ⇒2x+2 = 2 ; x= 0 ⇒2x+2 = (2/3) ; x<0

$$\:\:\mathrm{Let}\:{x}=\:{c}\:\:\mathrm{be}\:\mathrm{a}\:\mathrm{vertical}\:\mathrm{asymptot}\: \\ $$$$\:\:\underset{{x}\rightarrow{c}} {\mathrm{lim}}\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2x}+\mathrm{2}}\right)\:=\:\infty\: \\ $$$$\:\:\mathrm{it}\:\mathrm{follow}\:\mathrm{that}\:\frac{\pi}{\mathrm{2x}+\mathrm{2}}\:=\:\frac{\pi}{\mathrm{2}}\:\mathrm{or}\:\frac{\pi}{\mathrm{2x}+\mathrm{2}}\:=\:\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$$\:\:\Rightarrow\mathrm{2x}+\mathrm{2}\:=\:\mathrm{2}\:;\:\mathrm{x}=\:\mathrm{0} \\ $$$$\:\:\Rightarrow\mathrm{2x}+\mathrm{2}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:;\:\mathrm{x}<\mathrm{0}\: \\ $$

Commented by mnjuly1970 last updated on 18/Nov/24

$$\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com