Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 62610 by hovea cw last updated on 23/Jun/19

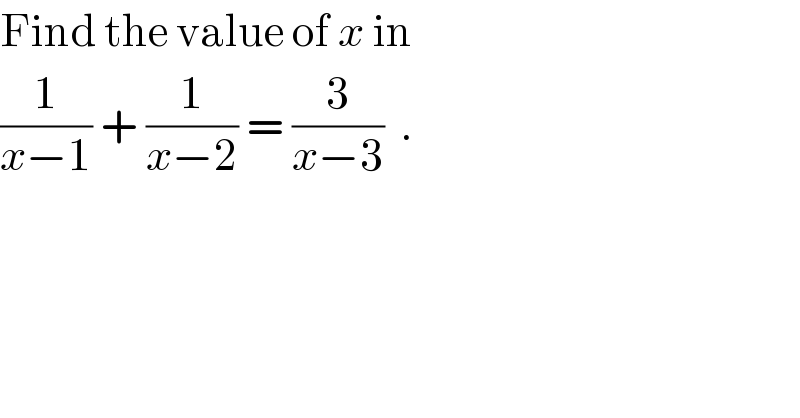
Find the value of x in (1/(x−1)) + (1/(x−2)) = (3/(x−3)) .

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{x}\:\mathrm{in} \\ $$$$\frac{\mathrm{1}}{{x}−\mathrm{1}}\:+\:\frac{\mathrm{1}}{{x}−\mathrm{2}}\:=\:\frac{\mathrm{3}}{{x}−\mathrm{3}}\:\:. \\ $$

Commented by mathmax by abdo last updated on 24/Jun/19

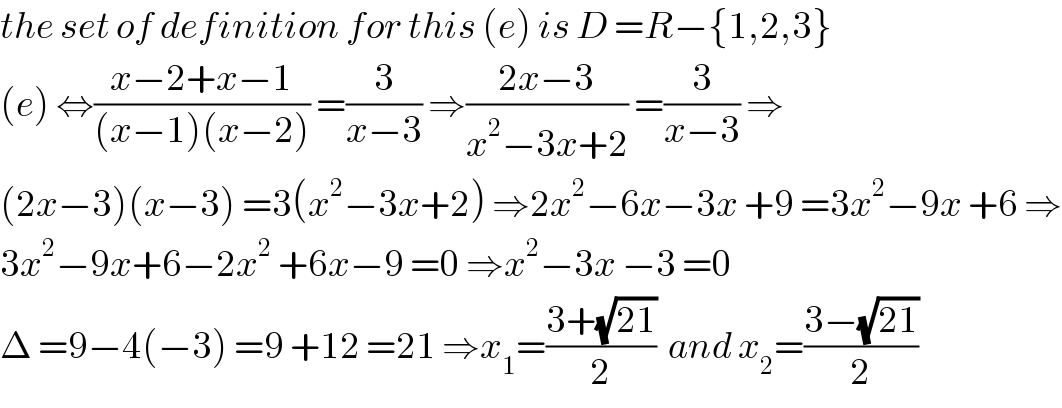
the set of definition for this (e) is D =R−{1,2,3} (e) ⇔((x−2+x−1)/((x−1)(x−2))) =(3/(x−3)) ⇒((2x−3)/(x^2 −3x+2)) =(3/(x−3)) ⇒ (2x−3)(x−3) =3(x^2 −3x+2) ⇒2x^2 −6x−3x +9 =3x^2 −9x +6 ⇒ 3x^2 −9x+6−2x^2 +6x−9 =0 ⇒x^2 −3x −3 =0 Δ =9−4(−3) =9 +12 =21 ⇒x_1 =((3+(√(21)))/2) and x_2 =((3−(√(21)))/2)

$${the}\:{set}\:{of}\:{definition}\:{for}\:{this}\:\left({e}\right)\:{is}\:{D}\:={R}−\left\{\mathrm{1},\mathrm{2},\mathrm{3}\right\} \\ $$$$\left({e}\right)\:\Leftrightarrow\frac{{x}−\mathrm{2}+{x}−\mathrm{1}}{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)}\:=\frac{\mathrm{3}}{{x}−\mathrm{3}}\:\Rightarrow\frac{\mathrm{2}{x}−\mathrm{3}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}}\:=\frac{\mathrm{3}}{{x}−\mathrm{3}}\:\Rightarrow \\ $$$$\left(\mathrm{2}{x}−\mathrm{3}\right)\left({x}−\mathrm{3}\right)\:=\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)\:\Rightarrow\mathrm{2}{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{3}{x}\:+\mathrm{9}\:=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{9}{x}\:+\mathrm{6}\:\Rightarrow \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{6}−\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{6}{x}−\mathrm{9}\:=\mathrm{0}\:\Rightarrow{x}^{\mathrm{2}} −\mathrm{3}{x}\:−\mathrm{3}\:=\mathrm{0} \\ $$$$\Delta\:=\mathrm{9}−\mathrm{4}\left(−\mathrm{3}\right)\:=\mathrm{9}\:+\mathrm{12}\:=\mathrm{21}\:\Rightarrow{x}_{\mathrm{1}} =\frac{\mathrm{3}+\sqrt{\mathrm{21}}}{\mathrm{2}}\:\:{and}\:{x}_{\mathrm{2}} =\frac{\mathrm{3}−\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$

Commented by $@ty@m last updated on 24/Jun/19

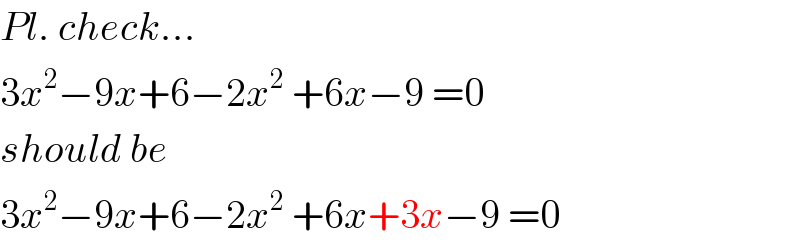
Pl. check... 3x^2 −9x+6−2x^2 +6x−9 =0 should be 3x^2 −9x+6−2x^2 +6x+3x−9 =0

$${Pl}.\:{check}... \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{6}−\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{6}{x}−\mathrm{9}\:=\mathrm{0} \\ $$$${should}\:{be} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{6}−\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{6}{x}+\mathrm{3}{x}−\mathrm{9}\:=\mathrm{0} \\ $$

Answered by $@ty@m last updated on 23/Jun/19

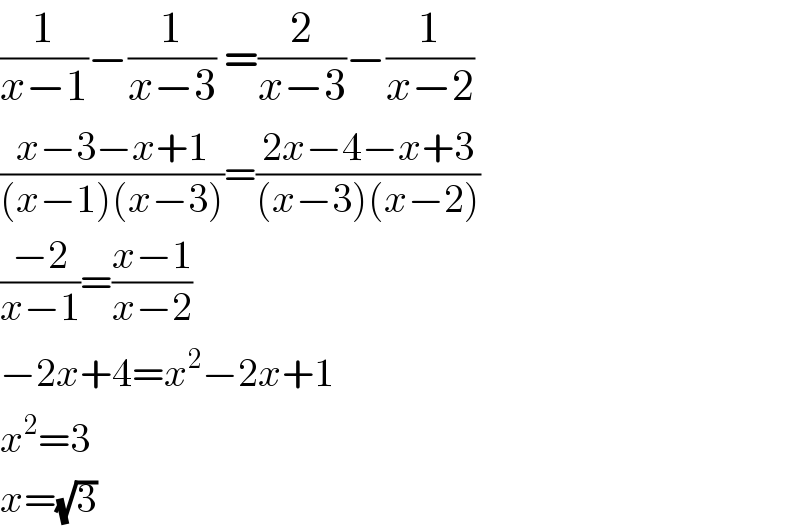
(1/(x−1))−(1/(x−3)) =(2/(x−3))−(1/(x−2)) ((x−3−x+1)/((x−1)(x−3)))=((2x−4−x+3)/((x−3)(x−2))) ((−2)/(x−1))=((x−1)/(x−2)) −2x+4=x^2 −2x+1 x^2 =3 x=(√3)

$$\frac{\mathrm{1}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{{x}−\mathrm{3}}\:=\frac{\mathrm{2}}{{x}−\mathrm{3}}−\frac{\mathrm{1}}{{x}−\mathrm{2}}\: \\ $$$$\frac{{x}−\mathrm{3}−{x}+\mathrm{1}}{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right)}=\frac{\mathrm{2}{x}−\mathrm{4}−{x}+\mathrm{3}}{\left({x}−\mathrm{3}\right)\left({x}−\mathrm{2}\right)} \\ $$$$\frac{−\mathrm{2}}{{x}−\mathrm{1}}=\frac{{x}−\mathrm{1}}{{x}−\mathrm{2}} \\ $$$$−\mathrm{2}{x}+\mathrm{4}={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1} \\ $$$${x}^{\mathrm{2}} =\mathrm{3} \\ $$$${x}=\sqrt{\mathrm{3}} \\ $$

Answered by MJS last updated on 23/Jun/19

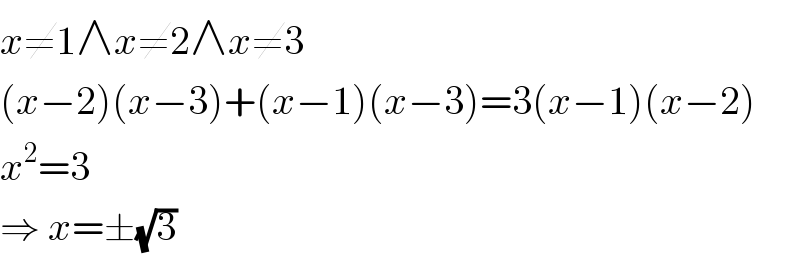
x≠1∧x≠2∧x≠3 (x−2)(x−3)+(x−1)(x−3)=3(x−1)(x−2) x^2 =3 ⇒ x=±(√3)

$${x}\neq\mathrm{1}\wedge{x}\neq\mathrm{2}\wedge{x}\neq\mathrm{3} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)+\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right)=\mathrm{3}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right) \\ $$$${x}^{\mathrm{2}} =\mathrm{3} \\ $$$$\Rightarrow\:{x}=\pm\sqrt{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com