Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 5385 by sanusihammed last updated on 12/May/16

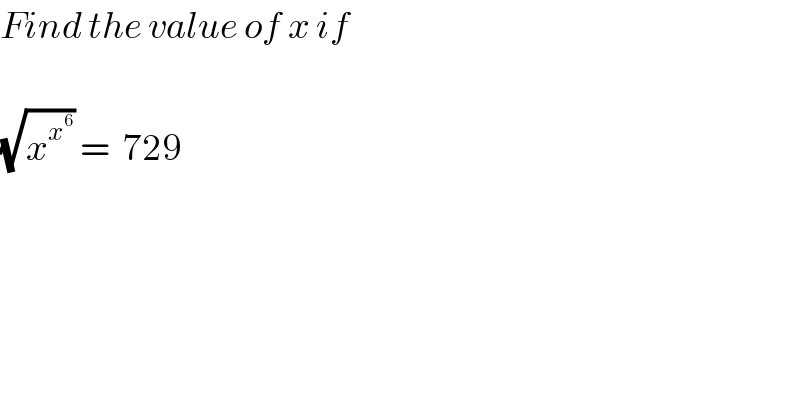
Find the value of x if (√x^x^6 ) = 729

$${Find}\:{the}\:{value}\:{of}\:{x}\:{if}\: \\ $$$$ \\ $$$$\sqrt{{x}^{{x}^{\mathrm{6}} } }\:=\:\:\mathrm{729} \\ $$

Answered by prakash jain last updated on 12/May/16

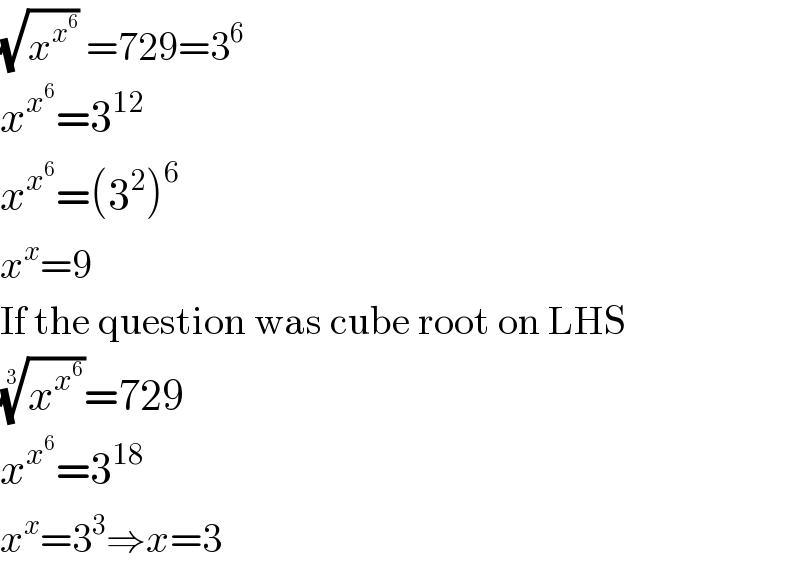
(√x^x^6 ) =729=3^6 x^x^6 =3^(12) x^x^6 =(3^2 )^6 x^x =9 If the question was cube root on LHS (x^x^6 )^(1/3) =729 x^x^6 =3^(18) x^x =3^3 ⇒x=3

$$\sqrt{{x}^{{x}^{\mathrm{6}} } }\:=\mathrm{729}=\mathrm{3}^{\mathrm{6}} \\ $$$${x}^{{x}^{\mathrm{6}} } =\mathrm{3}^{\mathrm{12}} \\ $$$${x}^{{x}^{\mathrm{6}} } =\left(\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{6}} \\ $$$${x}^{{x}} =\mathrm{9} \\ $$$$\mathrm{If}\:\mathrm{the}\:\mathrm{question}\:\mathrm{was}\:\mathrm{cube}\:\mathrm{root}\:\mathrm{on}\:\mathrm{LHS} \\ $$$$\sqrt[{\mathrm{3}}]{{x}^{{x}^{\mathrm{6}} } }=\mathrm{729} \\ $$$${x}^{{x}^{\mathrm{6}} } =\mathrm{3}^{\mathrm{18}} \\ $$$${x}^{{x}} =\mathrm{3}^{\mathrm{3}} \Rightarrow{x}=\mathrm{3} \\ $$

Commented by Rasheed Soomro last updated on 16/May/16

x^x^6 =^(?) (x^x )^6 Or x^x^6 =x^((x^6 )) ? x^x^6 =(3^2 )^6 ⇒^(?) x^x =9

$$\mathrm{x}^{\mathrm{x}^{\mathrm{6}} } \overset{?} {=}\:\left(\mathrm{x}^{\mathrm{x}} \right)^{\mathrm{6}} \\ $$$$\mathrm{Or}\:\mathrm{x}^{\mathrm{x}^{\mathrm{6}} } =\mathrm{x}^{\left(\mathrm{x}^{\mathrm{6}} \right)} \:? \\ $$$${x}^{{x}^{\mathrm{6}} } =\left(\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{6}} \overset{?} {\Rightarrow}{x}^{{x}} =\mathrm{9} \\ $$$$ \\ $$

Answered by Rasheed Soomro last updated on 15/May/16

(√x^x^6 ) = 729⇒x^((1/2)x^6 ) =729 −−−−−−−−−−−− To write 729 in the base of x x^■ =729 ■log_3 x=log_3 729=6 ■=(6/(log_3 x)) 729=x^(6/(log_3 x)) −−−−−−−−− x^((1/2)x^6 ) = x^(6/(log_3 x)) ⇒(1/2)x^6 =(6/(log_3 x)) (1/2)x^6 log_3 x=6 x^6 log_3 x=12 x^6 =((3×4)/(log_3 x))=((log_3 27 ×4)/(log_3 x))=((log_3 27^4 )/(log_3 x))=log_x 27^4 x^6 =log_x 27^4 Continue

$$\sqrt{{x}^{{x}^{\mathrm{6}} } }\:=\:\:\mathrm{729}\Rightarrow{x}^{\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{6}} } =\mathrm{729} \\ $$$$−−−−−−−−−−−− \\ $$$$\mathrm{To}\:\mathrm{write}\:\mathrm{729}\:\mathrm{in}\:\mathrm{the}\:\mathrm{base}\:\mathrm{of}\:\mathrm{x} \\ $$$${x}^{\blacksquare} =\mathrm{729} \\ $$$$\blacksquare\mathrm{log}_{\mathrm{3}} \:\mathrm{x}=\mathrm{log}_{\mathrm{3}} \mathrm{729}=\mathrm{6} \\ $$$$\blacksquare=\frac{\mathrm{6}}{\mathrm{log}_{\mathrm{3}} \:\mathrm{x}} \\ $$$$\mathrm{729}=\mathrm{x}^{\frac{\mathrm{6}}{\mathrm{log}_{\mathrm{3}} \:\mathrm{x}}} \\ $$$$−−−−−−−−− \\ $$$${x}^{\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{6}} } =\:\mathrm{x}^{\frac{\mathrm{6}}{\mathrm{log}_{\mathrm{3}} \:\mathrm{x}}} \Rightarrow\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{6}} =\frac{\mathrm{6}}{\mathrm{log}_{\mathrm{3}} \:\mathrm{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{6}} \:\mathrm{log}_{\mathrm{3}} \:\mathrm{x}=\mathrm{6} \\ $$$${x}^{\mathrm{6}} \mathrm{log}_{\mathrm{3}} \mathrm{x}=\mathrm{12} \\ $$$${x}^{\mathrm{6}} =\frac{\mathrm{3}×\mathrm{4}}{\mathrm{log}_{\mathrm{3}} \mathrm{x}}=\frac{\mathrm{log}_{\mathrm{3}} \mathrm{27}\:×\mathrm{4}}{\mathrm{log}_{\mathrm{3}} \mathrm{x}}=\frac{\mathrm{log}_{\mathrm{3}} \mathrm{27}^{\mathrm{4}} }{\mathrm{log}_{\mathrm{3}} \mathrm{x}}=\mathrm{log}_{\mathrm{x}} \mathrm{27}^{\mathrm{4}} \\ $$$$\mathrm{x}^{\mathrm{6}} =\mathrm{log}_{\mathrm{x}} \mathrm{27}^{\mathrm{4}} \\ $$$$\mathrm{Continue} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com