
Question Number 6838 by Tawakalitu. last updated on 30/Jul/16
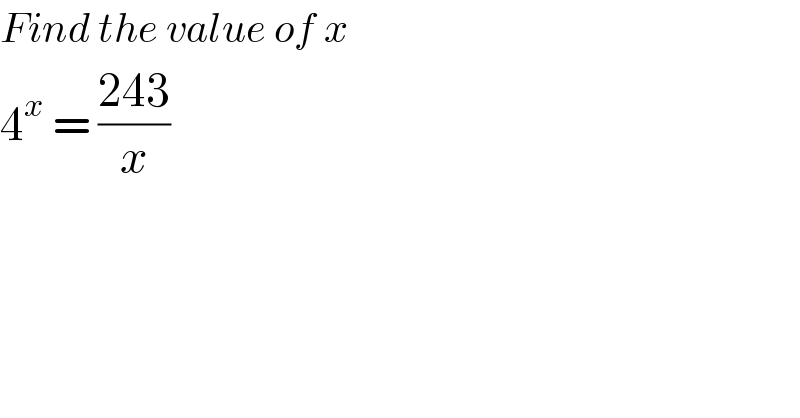
$${Find}\:{the}\:{value}\:{of}\:{x} \\ $$$$\mathrm{4}^{{x}} \:=\:\frac{\mathrm{243}}{{x}} \\ $$
Commented by Yozzii last updated on 31/Jul/16
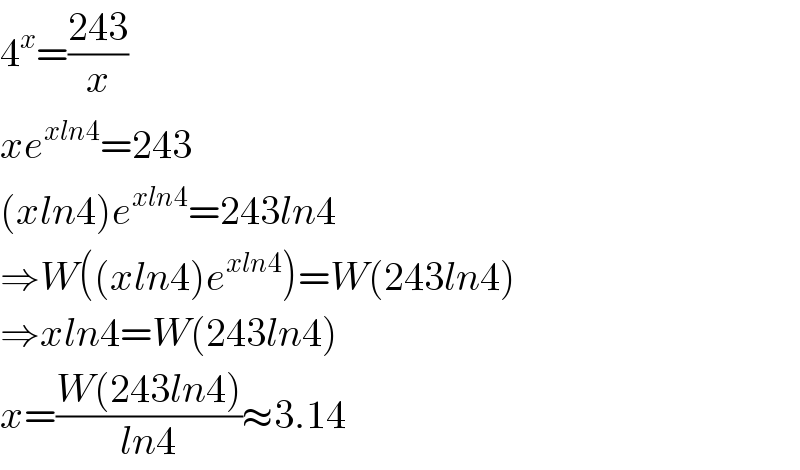
$$\mathrm{4}^{{x}} =\frac{\mathrm{243}}{{x}} \\ $$$${xe}^{{xln}\mathrm{4}} =\mathrm{243} \\ $$$$\left({xln}\mathrm{4}\right){e}^{{xln}\mathrm{4}} =\mathrm{243}{ln}\mathrm{4} \\ $$$$\Rightarrow{W}\left(\left({xln}\mathrm{4}\right){e}^{{xln}\mathrm{4}} \right)={W}\left(\mathrm{243}{ln}\mathrm{4}\right) \\ $$$$\Rightarrow{xln}\mathrm{4}={W}\left(\mathrm{243}{ln}\mathrm{4}\right) \\ $$$${x}=\frac{{W}\left(\mathrm{243}{ln}\mathrm{4}\right)}{{ln}\mathrm{4}}\approx\mathrm{3}.\mathrm{14} \\ $$
Commented by Tawakalitu. last updated on 31/Jul/16
$${i}\:{really}\:{appreciate}.\: \\ $$
