
Question Number 130465 by naka3546 last updated on 25/Jan/21
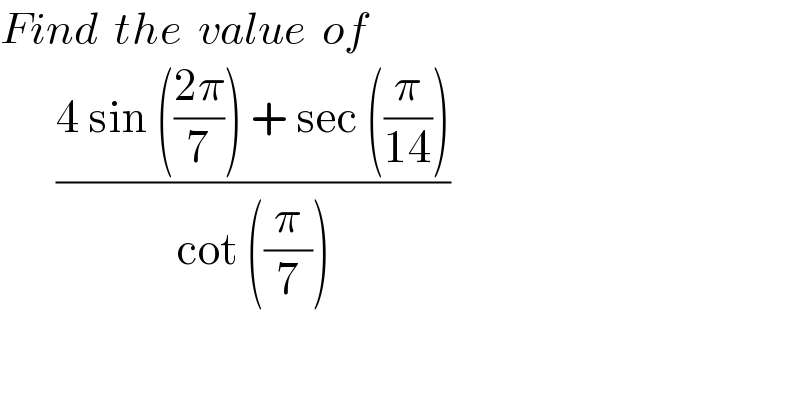
$${Find}\:\:{the}\:\:{value}\:\:{of} \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{4}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\:+\:\mathrm{sec}\:\left(\frac{\pi}{\mathrm{14}}\right)}{\mathrm{cot}\:\left(\frac{\pi}{\mathrm{7}}\right)} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Jan/21

$$\frac{\mathrm{4}{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right){cos}\left(\frac{\pi}{\mathrm{14}}\right){sin}\left(\frac{\pi}{\mathrm{7}}\right)+{sin}\left(\frac{\pi}{\mathrm{7}}\right)}{{cos}\frac{\pi}{\mathrm{7}}{cos}\frac{\pi}{\mathrm{14}}} \\ $$$$=\frac{\mathrm{2}{cos}\frac{\pi}{\mathrm{7}}{cos}\frac{\pi}{\mathrm{14}}−\mathrm{2}{cos}\frac{\mathrm{3}\pi}{\mathrm{7}}{cos}\frac{\pi}{\mathrm{14}}+{sin}\frac{\pi}{\mathrm{14}}}{{cos}\frac{\pi}{\mathrm{7}}{cos}\frac{\pi}{\mathrm{14}}} \\ $$$$=\mathrm{2}+\frac{−{cos}\left(\frac{\mathrm{7}\pi}{\mathrm{14}}\right)−{cos}\left(\frac{\mathrm{5}\pi}{\mathrm{14}}\right)+{sin}\left(\frac{\pi}{\mathrm{14}}\right)}{{cos}\frac{\pi}{\mathrm{7}}{cos}\frac{\pi}{\mathrm{14}}} \\ $$$$=\mathrm{2}+\frac{−\mathrm{0}+{sin}\left(\frac{\pi}{\mathrm{14}}\right)−{sin}\left(\frac{\pi}{\mathrm{14}}\right)}{{cos}\frac{\pi}{\mathrm{7}}{cos}\frac{\pi}{\mathrm{14}}}=\mathrm{2} \\ $$
Commented by naka3546 last updated on 26/Jan/21

$$\mathrm{thanks}\:,\:\mathrm{sir}. \\ $$
