Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 26067 by Joel578 last updated on 19/Dec/17

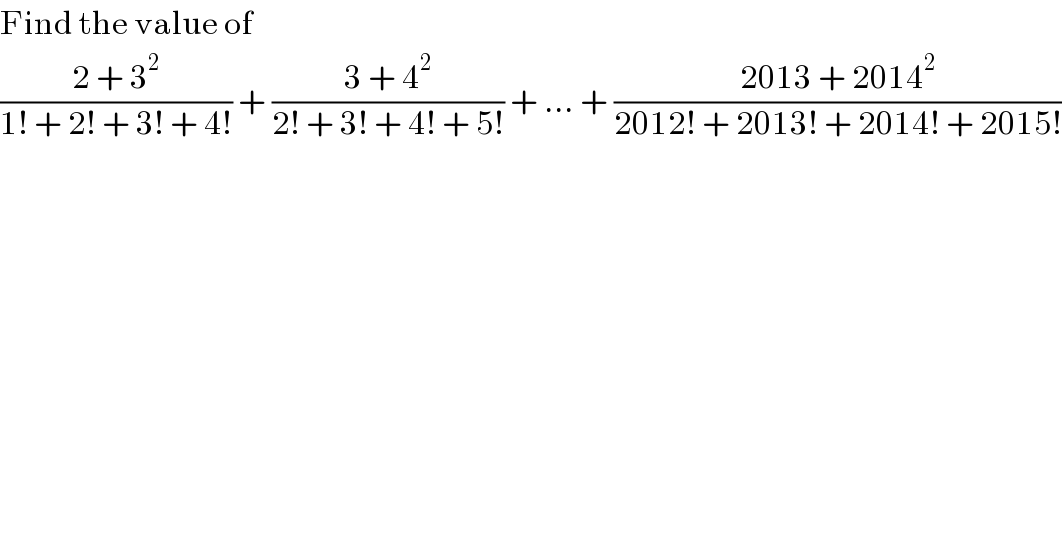
Find the value of ((2 + 3^2 )/(1! + 2! + 3! + 4!)) + ((3 + 4^2 )/(2! + 3! + 4! + 5!)) + ... + ((2013 + 2014^2 )/(2012! + 2013! + 2014! + 2015!))

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$$\frac{\mathrm{2}\:+\:\mathrm{3}^{\mathrm{2}} }{\mathrm{1}!\:+\:\mathrm{2}!\:+\:\mathrm{3}!\:+\:\mathrm{4}!}\:+\:\frac{\mathrm{3}\:+\:\mathrm{4}^{\mathrm{2}} }{\mathrm{2}!\:+\:\mathrm{3}!\:+\:\mathrm{4}!\:+\:\mathrm{5}!}\:+\:...\:+\:\frac{\mathrm{2013}\:+\:\mathrm{2014}^{\mathrm{2}} }{\mathrm{2012}!\:+\:\mathrm{2013}!\:+\:\mathrm{2014}!\:+\:\mathrm{2015}!} \\ $$

Answered by iv@0uja last updated on 19/Dec/17

((2 + 3^2 )/(1! + 2! + 3! + 4!)) + ((3 + 4^2 )/(2! + 3! + 4! + 5!)) + ... + ((2013 + 2014^2 )/(2012! + 2013! + 2014! + 2015!)) =Σ_(n=1) ^(2012) ((n+1+(n+2)^2 )/(n!+(n+1)!+(n+2)!+(n+3)!)) =Σ_(n=1) ^(2012) ((n+1+(n+2)^2 )/(n!{1+(n+1)+(n+1)(n+2)+(n+1)(n+2)(n+3)})) =Σ_(n=1) ^(2012) ((n+1+(n+2)^2 )/(n!(n^3 +7n^2 +15n+10))) =Σ_(n=1) ^(2012) ((n^2 +5n+5)/(n!(n+2)(n^2 +5n+5))) =Σ_(n=1) ^(2012) (1/(n!(n+2))) =Σ_(n=1) ^(2012) ((1/((n+1)!))−(1/((n+2)!))) =((1/(2!))−(1/(3!)))+((1/(3!))−(1/(4!)))...((1/(2013!))−(1/(2014!))) =(1/2)−(1/(2014!))

$$\:\:\:\:\:\frac{\mathrm{2}\:+\:\mathrm{3}^{\mathrm{2}} }{\mathrm{1}!\:+\:\mathrm{2}!\:+\:\mathrm{3}!\:+\:\mathrm{4}!}\:+\:\frac{\mathrm{3}\:+\:\mathrm{4}^{\mathrm{2}} }{\mathrm{2}!\:+\:\mathrm{3}!\:+\:\mathrm{4}!\:+\:\mathrm{5}!}\:+\:...\:+\:\frac{\mathrm{2013}\:+\:\mathrm{2014}^{\mathrm{2}} }{\mathrm{2012}!\:+\:\mathrm{2013}!\:+\:\mathrm{2014}!\:+\:\mathrm{2015}!} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2012}} {\sum}}\frac{{n}+\mathrm{1}+\left({n}+\mathrm{2}\right)^{\mathrm{2}} }{{n}!+\left({n}+\mathrm{1}\right)!+\left({n}+\mathrm{2}\right)!+\left({n}+\mathrm{3}\right)!} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2012}} {\sum}}\frac{{n}+\mathrm{1}+\left({n}+\mathrm{2}\right)^{\mathrm{2}} }{{n}!\left\{\mathrm{1}+\left({n}+\mathrm{1}\right)+\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)+\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)\right\}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2012}} {\sum}}\frac{{n}+\mathrm{1}+\left({n}+\mathrm{2}\right)^{\mathrm{2}} }{{n}!\left({n}^{\mathrm{3}} +\mathrm{7}{n}^{\mathrm{2}} +\mathrm{15}{n}+\mathrm{10}\right)} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2012}} {\sum}}\frac{{n}^{\mathrm{2}} +\mathrm{5}{n}+\mathrm{5}}{{n}!\left({n}+\mathrm{2}\right)\left({n}^{\mathrm{2}} +\mathrm{5}{n}+\mathrm{5}\right)} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2012}} {\sum}}\frac{\mathrm{1}}{{n}!\left({n}+\mathrm{2}\right)} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2012}} {\sum}}\left(\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}−\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)!}\right) \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}!}−\frac{\mathrm{1}}{\mathrm{4}!}\right)...\left(\frac{\mathrm{1}}{\mathrm{2013}!}−\frac{\mathrm{1}}{\mathrm{2014}!}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2014}!} \\ $$

Commented by Joel578 last updated on 19/Dec/17

thank you very much

$${thank}\:{you}\:{very}\:{much} \\ $$

Answered by ajfour last updated on 19/Dec/17

T_r =((r+1+r^2 +4r+4)/D_r )=((r^2 +5r+5)/D_r ) D_r =r!+(r+1)!+(r+2)!+(r+3)! =r!(1+r+1+r^2 +3r+2+ r^3 +6r^2 +11r+6) D_r = r!(r^3 +7r^2 +15r+10) =r!(r+2)(r^2 +5r+5)] ⇒ T_r =(1/(r!(r+2))) =((r+1)/((r+2)!)) = (((r+2)−1)/((r+2)!)) = (1/((r+1)!))−(1/((r+2)!)) S=Σ_1 ^(2012) T_r =((1/(2!))−(1/(3!)))+((1/(3!))−(1/(4!)))+ ((1/(4!))−(1/(5!)))+.....+((1/(2013!))−(1/(2014!))) Hence S =(1/(2!))−(1/(2014!)) .

$${T}_{{r}} =\frac{{r}+\mathrm{1}+{r}^{\mathrm{2}} +\mathrm{4}{r}+\mathrm{4}}{{D}_{{r}} }=\frac{{r}^{\mathrm{2}} +\mathrm{5}{r}+\mathrm{5}}{{D}_{{r}} } \\ $$$${D}_{{r}} ={r}!+\left({r}+\mathrm{1}\right)!+\left({r}+\mathrm{2}\right)!+\left({r}+\mathrm{3}\right)! \\ $$$$\:\:\:\:\:={r}!\left(\mathrm{1}+{r}+\mathrm{1}+{r}^{\mathrm{2}} +\mathrm{3}{r}+\mathrm{2}+\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{r}^{\mathrm{3}} +\mathrm{6}{r}^{\mathrm{2}} +\mathrm{11}{r}+\mathrm{6}\right) \\ $$$$\:{D}_{{r}} =\:{r}!\left({r}^{\mathrm{3}} +\mathrm{7}{r}^{\mathrm{2}} +\mathrm{15}{r}+\mathrm{10}\right) \\ $$$$\left.\:\:\:\:\:\:={r}!\left({r}+\mathrm{2}\right)\left({r}^{\mathrm{2}} +\mathrm{5}{r}+\mathrm{5}\right)\right] \\ $$$$\Rightarrow\:{T}_{{r}} =\frac{\mathrm{1}}{{r}!\left({r}+\mathrm{2}\right)}\:=\frac{{r}+\mathrm{1}}{\left({r}+\mathrm{2}\right)!} \\ $$$$\:\:\:\:=\:\frac{\left({r}+\mathrm{2}\right)−\mathrm{1}}{\left({r}+\mathrm{2}\right)!}\:=\:\frac{\mathrm{1}}{\left({r}+\mathrm{1}\right)!}−\frac{\mathrm{1}}{\left({r}+\mathrm{2}\right)!} \\ $$$${S}=\underset{\mathrm{1}} {\overset{\mathrm{2012}} {\sum}}{T}_{{r}} \:=\left(\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}!}−\frac{\mathrm{1}}{\mathrm{4}!}\right)+ \\ $$$$\:\:\:\:\:\left(\frac{\mathrm{1}}{\mathrm{4}!}−\frac{\mathrm{1}}{\mathrm{5}!}\right)+.....+\left(\frac{\mathrm{1}}{\mathrm{2013}!}−\frac{\mathrm{1}}{\mathrm{2014}!}\right) \\ $$$$\:\:{Hence}\:\:{S}\:=\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{2014}!}\:. \\ $$

Commented by Joel578 last updated on 19/Dec/17

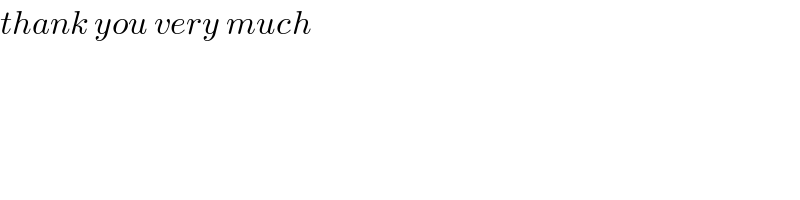
thank you very much

$${thank}\:{you}\:{very}\:{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com