
Question Number 67298 by Rio Michael last updated on 25/Aug/19

$${Find}\:\:{the}\:{third}\:{degree}\:{polynomial}\:{which}\:{vanishes}\:{when} \\ $$$${x}\:=−\mathrm{1}\:{and}\:{x}\:=\:\mathrm{2},\:{which}\:{has}\:{a}\:{value}\:\mathrm{8}\:{when}\:{x}\:=\mathrm{0}\:{and}\:{leaves}\:{a}\:{remainder}\:\frac{\mathrm{16}}{\mathrm{3}}\:{when} \\ $$$${divided}\:{by}\:\:\mathrm{3}{x}\:+\:\mathrm{2}. \\ $$
Commented by Prithwish sen last updated on 25/Aug/19
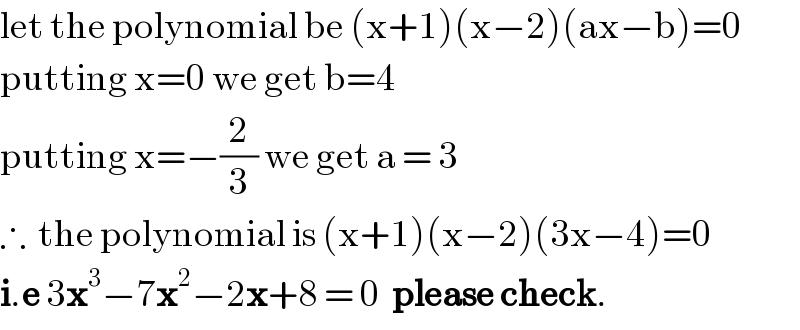
$$\mathrm{let}\:\mathrm{the}\:\mathrm{polynomial}\:\mathrm{be}\:\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{ax}−\mathrm{b}\right)=\mathrm{0} \\ $$$$\mathrm{putting}\:\mathrm{x}=\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:\mathrm{b}=\mathrm{4} \\ $$$$\mathrm{putting}\:\mathrm{x}=−\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:=\:\mathrm{3} \\ $$$$\therefore\:\:\mathrm{the}\:\mathrm{polynomial}\:\mathrm{is}\:\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{3x}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{i}}.\boldsymbol{\mathrm{e}}\:\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{3}} −\mathrm{7}\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{x}}+\mathrm{8}\:=\:\mathrm{0}\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by Rio Michael last updated on 25/Aug/19
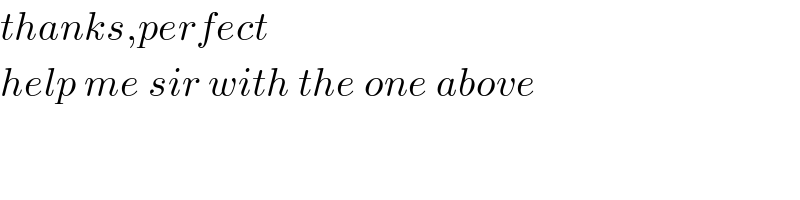
$${thanks},{perfect} \\ $$$${help}\:{me}\:{sir}\:{with}\:{the}\:{one}\:{above} \\ $$
