
Question Number 85532 by oustmuchiya@gmail.com last updated on 22/Mar/20

$${Find}\:{the}\:{term}\:{independent}\:{of}\:\boldsymbol{\mathrm{x}}\:{in}\:{the}\:{expression}\:{of}\:\left(\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{2}{x}}\right)^{\mathrm{9}} \\ $$
Answered by mind is power last updated on 22/Mar/20
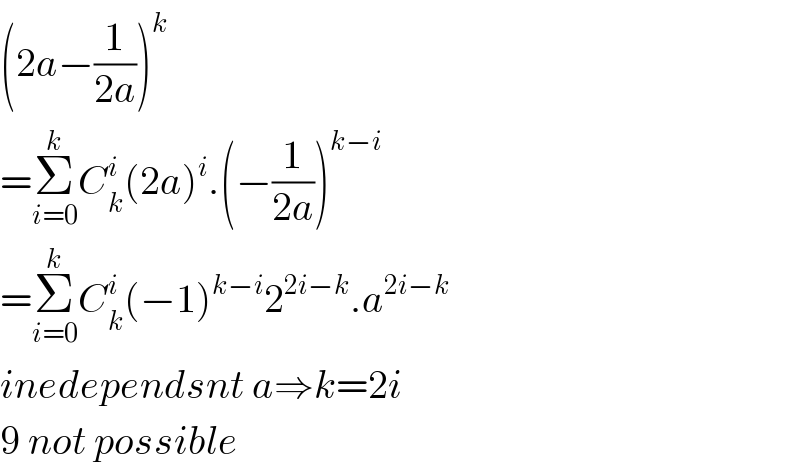
$$\left(\mathrm{2}{a}−\frac{\mathrm{1}}{\mathrm{2}{a}}\right)^{{k}} \\ $$$$=\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}{C}_{{k}} ^{{i}} \left(\mathrm{2}{a}\right)^{{i}} .\left(−\frac{\mathrm{1}}{\mathrm{2}{a}}\right)^{{k}−{i}} \\ $$$$=\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}{C}_{{k}} ^{{i}} \left(−\mathrm{1}\right)^{{k}−{i}} \mathrm{2}^{\mathrm{2}{i}−{k}} .{a}^{\mathrm{2}{i}−{k}} \\ $$$${inedependsnt}\:{a}\Rightarrow{k}=\mathrm{2}{i} \\ $$$$\mathrm{9}\:{not}\:{possible} \\ $$
Commented by jagoll last updated on 23/Mar/20

$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{got}\:\mathrm{same}\:\mathrm{result}.\: \\ $$$$\mathrm{nothing}\:\mathrm{independent}\:\mathrm{term}\:\mathrm{of}\:\mathrm{x} \\ $$
