
Question Number 115516 by bobhans last updated on 26/Sep/20
![Find the supremum and the infimum of (x/(sin x)) on the interval (0, (π/2) ]](Q115516.png)
$${Find}\:{the}\:{supremum}\:{and}\:{the}\:{infimum} \\ $$$${of}\:\frac{{x}}{\mathrm{sin}\:{x}}\:{on}\:{the}\:{interval}\:\left(\mathrm{0},\:\frac{\pi}{\mathrm{2}}\:\right] \\ $$
Commented by john santu last updated on 26/Sep/20
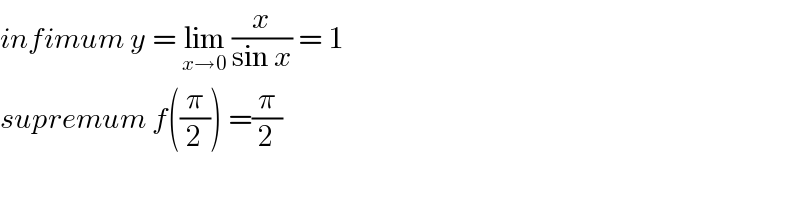
$${infimum}\:{y}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}}{\mathrm{sin}\:{x}}\:=\:\mathrm{1} \\ $$$${supremum}\:{f}\left(\frac{\pi}{\mathrm{2}}\right)\:=\frac{\pi}{\mathrm{2}} \\ $$
Answered by TANMAY PANACEA last updated on 26/Sep/20
![y=(x/(sinx)) (dy/dx)=((sinx−xcosx)/(sin^2 x)) for max\min (dy/dx)=0 so x=tanx (d^2 y/dx^2 )=((sin^2 x(cosx−cosx+xsinx)−(sinx−xcosx)(2sinxcosx))/(sin^4 x)) (d^2 y/dx^2 )=((xsin^3 x−2sin^2 xcosx+2xsinxcos^2 x)/(sin^4 x)) now putting x=tanx in (d^2 y/dx^2 ) ((d^2 y/dx^2 ))_(x=tanx) =((((sin^4 x)/(cosx))−2sin^2 xcosx+2sin^2 xcosx)/(sin^4 x)) ((d^2 y/dx^2 ))_(x=tanx) =secx>0 when x∈(0,(π/2)] wait...](Q115536.png)
$${y}=\frac{{x}}{{sinx}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{sinx}−{xcosx}}{{sin}^{\mathrm{2}} {x}} \\ $$$$ \\ $$$${for}\:{max}\backslash{min}\:\:\frac{{dy}}{{dx}}=\mathrm{0}\:\:\:{so}\:{x}={tanx} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{sin}^{\mathrm{2}} {x}\left({cosx}−{cosx}+{xsinx}\right)−\left({sinx}−{xcosx}\right)\left(\mathrm{2}{sinxcosx}\right)}{{sin}^{\mathrm{4}} {x}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{xsin}^{\mathrm{3}} {x}−\mathrm{2}{sin}^{\mathrm{2}} {xcosx}+\mathrm{2}{xsinxcos}^{\mathrm{2}} {x}}{{sin}^{\mathrm{4}} {x}} \\ $$$${now}\:{putting}\:{x}={tanx}\:{in}\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} } \\ $$$$\left(\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right)_{{x}={tanx}} \:=\frac{\frac{{sin}^{\mathrm{4}} {x}}{{cosx}}−\mathrm{2}{sin}^{\mathrm{2}} {xcosx}+\mathrm{2}{sin}^{\mathrm{2}} {xcosx}}{{sin}^{\mathrm{4}} {x}} \\ $$$$\left(\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right)_{{x}={tanx}} ={secx}>\mathrm{0}\:\:\:{when}\:{x}\in\left(\mathrm{0},\frac{\pi}{\mathrm{2}}\right] \\ $$$${wait}... \\ $$
