Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 46860 by 786786AM last updated on 01/Nov/18

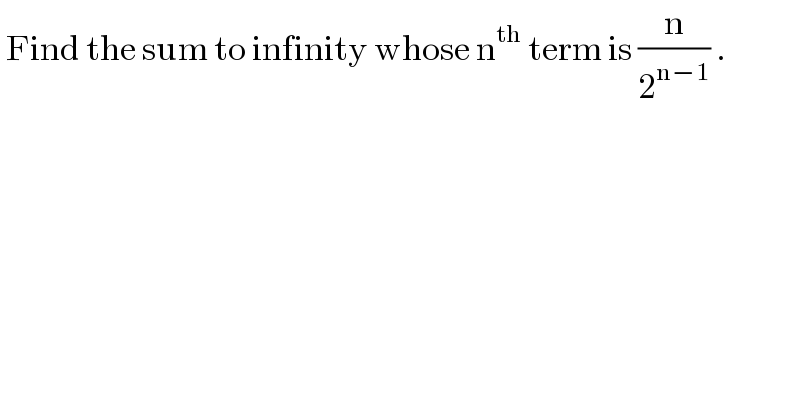
Find the sum to infinity whose n^(th) term is (n/2^(n−1) ) .

$$\:\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{to}\:\mathrm{infinity}\:\mathrm{whose}\:\mathrm{n}^{\mathrm{th}} \:\mathrm{term}\:\mathrm{is}\:\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} }\:. \\ $$

Commented by maxmathsup by imad last updated on 01/Nov/18

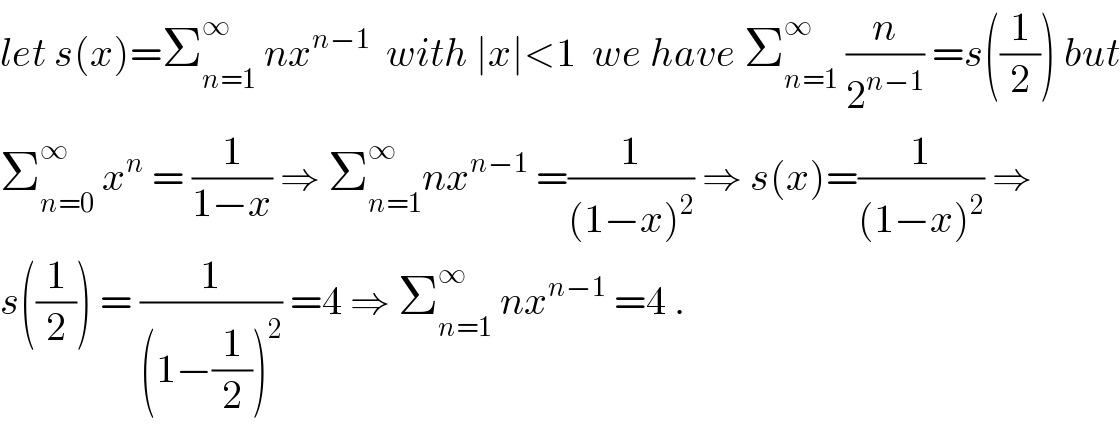
let s(x)=Σ_(n=1) ^∞ nx^(n−1) with ∣x∣<1 we have Σ_(n=1) ^∞ (n/2^(n−1) ) =s((1/2)) but Σ_(n=0) ^∞ x^n = (1/(1−x)) ⇒ Σ_(n=1) ^∞ nx^(n−1) =(1/((1−x)^2 )) ⇒ s(x)=(1/((1−x)^2 )) ⇒ s((1/2)) = (1/((1−(1/2))^2 )) =4 ⇒ Σ_(n=1) ^∞ nx^(n−1) =4 .

$${let}\:{s}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}−\mathrm{1}} \:\:{with}\:\mid{x}\mid<\mathrm{1}\:\:{we}\:{have}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} }\:={s}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:{but} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\Rightarrow\:\sum_{{n}=\mathrm{1}} ^{\infty} {nx}^{{n}−\mathrm{1}} \:=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow\:{s}\left({x}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${s}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\frac{\mathrm{1}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:=\mathrm{4}\:\Rightarrow\:\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}−\mathrm{1}} \:=\mathrm{4}\:. \\ $$

Commented by maxmathsup by imad last updated on 02/Nov/18

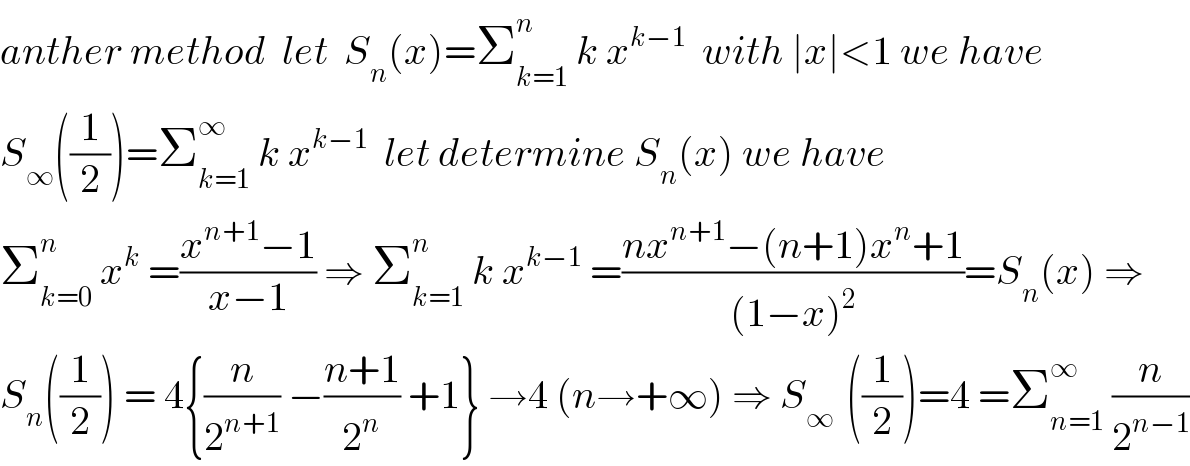
anther method let S_n (x)=Σ_(k=1) ^n k x^(k−1) with ∣x∣<1 we have S_∞ ((1/2))=Σ_(k=1) ^∞ k x^(k−1) let determine S_n (x) we have Σ_(k=0) ^n x^k =((x^(n+1) −1)/(x−1)) ⇒ Σ_(k=1) ^n k x^(k−1) =((nx^(n+1) −(n+1)x^n +1)/((1−x)^2 ))=S_n (x) ⇒ S_n ((1/2)) = 4{(n/2^(n+1) ) −((n+1)/2^n ) +1} →4 (n→+∞) ⇒ S_(∞ ) ((1/2))=4 =Σ_(n=1) ^∞ (n/2^(n−1) )

$${anther}\:{method}\:\:{let}\:\:{S}_{{n}} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:{x}^{{k}−\mathrm{1}} \:\:{with}\:\mid{x}\mid<\mathrm{1}\:{we}\:{have} \\ $$$${S}_{\infty} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sum_{{k}=\mathrm{1}} ^{\infty} \:{k}\:{x}^{{k}−\mathrm{1}} \:\:{let}\:{determine}\:{S}_{{n}} \left({x}\right)\:{we}\:{have} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{x}^{{k}} \:=\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\:\Rightarrow\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:{x}^{{k}−\mathrm{1}} \:=\frac{{nx}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }={S}_{{n}} \left({x}\right)\:\Rightarrow \\ $$$${S}_{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\mathrm{4}\left\{\frac{{n}}{\mathrm{2}^{{n}+\mathrm{1}} }\:−\frac{{n}+\mathrm{1}}{\mathrm{2}^{{n}} }\:+\mathrm{1}\right\}\:\rightarrow\mathrm{4}\:\left({n}\rightarrow+\infty\right)\:\Rightarrow\:{S}_{\infty\:} \:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{4}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} } \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 01/Nov/18

S_n =(1/2^0 )+(2/2^1 )+(3/2^2 )+(4/2^3 )+...+(n/2^(n−1) ) (S_n /2)= +(1/2^1 )+(2/2^2 )+(3/2^3 )+...+((n−1)/2^(n−1) )+(n/2^n ) S_n −(S_n /2)=((1/2^0 )+(1/2^1 )+(1/2^2 )+...+(1/2^(n−1) ))−(n/2^n ) (S_n /2)=(((1/2^0 )(1−(1/2^n )))/(1−(1/2)))−(n/2^n ) S_n = 2×(((1−(1/2^n )))/(1/2))−(n/2^n ) when n→∞ S_∞ =4

$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{3}} }+...+\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} } \\ $$$$\frac{{S}_{{n}} }{\mathrm{2}}=\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+...+\frac{{n}−\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }+\frac{{n}}{\mathrm{2}^{{n}} } \\ $$$${S}_{{n}} −\frac{{S}_{{n}} }{\mathrm{2}}=\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+...+\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\right)−\frac{{n}}{\mathrm{2}^{{n}} } \\ $$$$\frac{{S}_{{n}} }{\mathrm{2}}=\frac{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}−\frac{{n}}{\mathrm{2}^{{n}} } \\ $$$${S}_{{n}} =\:\mathrm{2}×\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)}{\frac{\mathrm{1}}{\mathrm{2}}}−\frac{{n}}{\mathrm{2}^{{n}} } \\ $$$${when}\:{n}\rightarrow\infty\:\:{S}_{\infty} \:=\mathrm{4} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com