
Question Number 198919 by necx122 last updated on 25/Oct/23
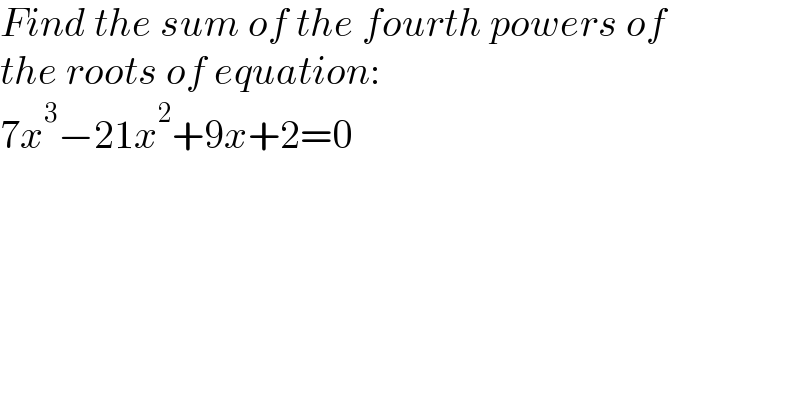
$${Find}\:{the}\:{sum}\:{of}\:{the}\:{fourth}\:{powers}\:{of} \\ $$$${the}\:{roots}\:{of}\:{equation}: \\ $$$$\mathrm{7}{x}^{\mathrm{3}} −\mathrm{21}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{2}=\mathrm{0} \\ $$
Commented by necx122 last updated on 25/Oct/23
wow! Really learning new things. Thank you sir.
Answered by deleteduser1 last updated on 25/Oct/23
![Let roots be a,b,c,. Then a+b+c=((−(−21))/7)=3 ab+bc+ca=(9/7);abc=((−2)/7) a^4 +b^4 +c^4 =(a^2 +b^2 +c^2 )^2 −2[(ab)^2 +(bc)^2 +(ca)^2 ] (a^2 +b^2 +c^2 )=(a+b+c)^2 −2(ab+bc+ca)=9−((18)/7) =((63−18)/7)=((45)/7) (ab)^2 +(bc)^2 +(ca)^2 =[ab+bc+ca]^2 −2abc(a+b+c) =((81)/(49))+((84)/(49))=((165)/(49)) ⇒a^4 +b^4 +c^4 =(((45)/7))^2 −((330)/(49))=((1695)/(49))](Q198923.png)
$${Let}\:{roots}\:{be}\:{a},{b},{c},.\:{Then}\:{a}+{b}+{c}=\frac{−\left(−\mathrm{21}\right)}{\mathrm{7}}=\mathrm{3} \\ $$$${ab}+{bc}+{ca}=\frac{\mathrm{9}}{\mathrm{7}};{abc}=\frac{−\mathrm{2}}{\mathrm{7}} \\ $$$$ \\ $$$${a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} =\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left[\left({ab}\right)^{\mathrm{2}} +\left({bc}\right)^{\mathrm{2}} +\left({ca}\right)^{\mathrm{2}} \right] \\ $$$$\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)=\left({a}+{b}+{c}\right)^{\mathrm{2}} −\mathrm{2}\left({ab}+{bc}+{ca}\right)=\mathrm{9}−\frac{\mathrm{18}}{\mathrm{7}} \\ $$$$=\frac{\mathrm{63}−\mathrm{18}}{\mathrm{7}}=\frac{\mathrm{45}}{\mathrm{7}} \\ $$$$\left({ab}\right)^{\mathrm{2}} +\left({bc}\right)^{\mathrm{2}} +\left({ca}\right)^{\mathrm{2}} =\left[{ab}+{bc}+{ca}\right]^{\mathrm{2}} −\mathrm{2}{abc}\left({a}+{b}+{c}\right) \\ $$$$=\frac{\mathrm{81}}{\mathrm{49}}+\frac{\mathrm{84}}{\mathrm{49}}=\frac{\mathrm{165}}{\mathrm{49}} \\ $$$$\Rightarrow{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} =\left(\frac{\mathrm{45}}{\mathrm{7}}\right)^{\mathrm{2}} −\frac{\mathrm{330}}{\mathrm{49}}=\frac{\mathrm{1695}}{\mathrm{49}} \\ $$
