
Question Number 46697 by KMA last updated on 30/Oct/18
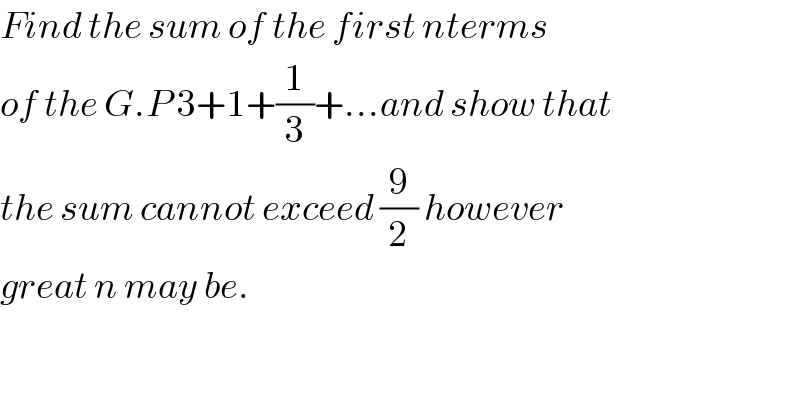
$${Find}\:{the}\:{sum}\:{of}\:{the}\:{first}\:{nterms}\: \\ $$$${of}\:{the}\:{G}.{P}\:\mathrm{3}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+...{and}\:{show}\:{that} \\ $$$${the}\:{sum}\:{cannot}\:{exceed}\:\frac{\mathrm{9}}{\mathrm{2}}\:{however} \\ $$$${great}\:{n}\:{may}\:{be}. \\ $$
Answered by Joel578 last updated on 30/Oct/18
![S_n = ((a(1 − r^n ))/( 1 − r)) = ((3(1 − ((1/3))^n ))/(1 − (1/3))) = (9/2)(1 − ((1/3))^n ) lim_(n→∞) S_n = lim_(n→∞) [(9/2)(1 − ((1/3))^n )] = (9/2) . lim_(n→∞) (1 − ((1/3))^n ) = (9/2)(1 − 0) = (9/2) It is showed that as n goes larger and larger, its value getting closer to (9/2) and never exceed (9/2)](Q46701.png)
$${S}_{{n}} \:=\:\frac{{a}\left(\mathrm{1}\:−\:{r}^{{n}} \right)}{\:\mathrm{1}\:−\:{r}}\:=\:\frac{\mathrm{3}\left(\mathrm{1}\:−\:\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} \right)}{\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:=\:\frac{\mathrm{9}}{\mathrm{2}}\left(\mathrm{1}\:−\:\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} \right) \\ $$$$ \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{S}_{{n}} \:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left[\frac{\mathrm{9}}{\mathrm{2}}\left(\mathrm{1}\:−\:\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} \right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{9}}{\mathrm{2}}\:.\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:−\:\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{9}}{\mathrm{2}}\left(\mathrm{1}\:−\:\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{showed}\:\mathrm{that}\:\mathrm{as}\:{n}\:\mathrm{goes}\:\mathrm{larger}\:\mathrm{and}\:\mathrm{larger}, \\ $$$$\mathrm{its}\:\mathrm{value}\:\mathrm{getting}\:\mathrm{closer}\:\mathrm{to}\:\:\frac{\mathrm{9}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{never}\:\mathrm{exceed}\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$
