
Question Number 48795 by rahul 19 last updated on 28/Nov/18
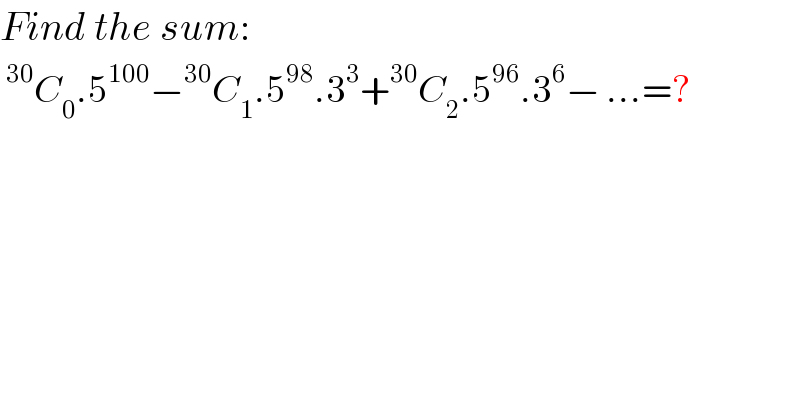
$${Find}\:{the}\:{sum}: \\ $$$$\:^{\mathrm{30}} {C}_{\mathrm{0}} .\mathrm{5}^{\mathrm{100}} −^{\mathrm{30}} {C}_{\mathrm{1}} .\mathrm{5}^{\mathrm{98}} .\mathrm{3}^{\mathrm{3}} +^{\mathrm{30}} {C}_{\mathrm{2}} .\mathrm{5}^{\mathrm{96}} .\mathrm{3}^{\mathrm{6}} −\:...=? \\ $$
Commented by rahul 19 last updated on 29/Nov/18
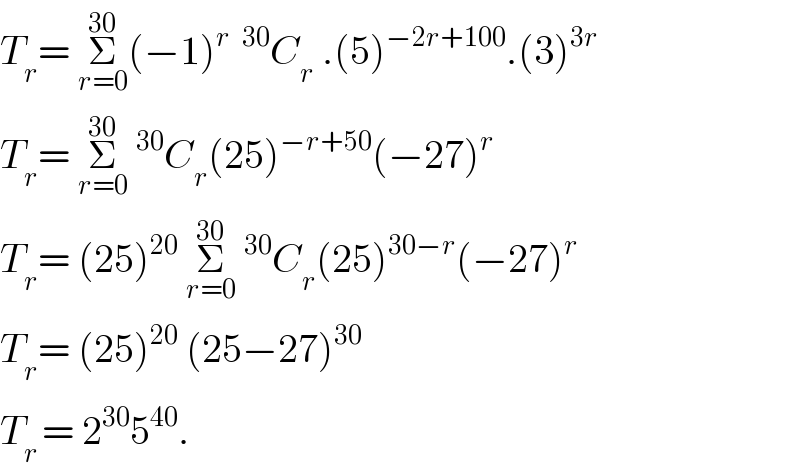
$${T}_{{r}} =\:\underset{{r}=\mathrm{0}} {\overset{\mathrm{30}} {\sum}}\left(−\mathrm{1}\right)^{{r}\:\:\:\mathrm{30}} {C}_{{r}} \:.\left(\mathrm{5}\right)^{−\mathrm{2}{r}+\mathrm{100}} .\left(\mathrm{3}\right)^{\mathrm{3}{r}} \\ $$$${T}_{{r}} =\:\underset{{r}=\mathrm{0}} {\overset{\mathrm{30}} {\sum}}\:^{\mathrm{30}} {C}_{{r}} \left(\mathrm{25}\right)^{−{r}+\mathrm{50}} \left(−\mathrm{27}\right)^{{r}} \\ $$$${T}_{{r}} =\:\left(\mathrm{25}\right)^{\mathrm{20}} \:\underset{{r}=\mathrm{0}} {\overset{\mathrm{30}} {\sum}}\:^{\mathrm{30}} {C}_{{r}} \left(\mathrm{25}\right)^{\mathrm{30}−{r}} \left(−\mathrm{27}\right)^{{r}} \\ $$$${T}_{{r}} =\:\left(\mathrm{25}\right)^{\mathrm{20}} \:\left(\mathrm{25}−\mathrm{27}\right)^{\mathrm{30}} \\ $$$${T}_{{r}\:} =\:\mathrm{2}^{\mathrm{30}} \mathrm{5}^{\mathrm{40}} . \\ $$
Answered by ajfour last updated on 28/Nov/18
![=(25)^(20) [^(30) C_0 (25)^(30) −^(30) C_1 (25)^(29) (27)+..] = (25)^(20) (25−27)^(30) = 2^(30) 5^(40) .](Q48797.png)
$$=\left(\mathrm{25}\right)^{\mathrm{20}} \left[\:^{\mathrm{30}} {C}_{\mathrm{0}} \left(\mathrm{25}\right)^{\mathrm{30}} −^{\mathrm{30}} {C}_{\mathrm{1}} \left(\mathrm{25}\right)^{\mathrm{29}} \left(\mathrm{27}\right)+..\right] \\ $$$$=\:\left(\mathrm{25}\right)^{\mathrm{20}} \left(\mathrm{25}−\mathrm{27}\right)^{\mathrm{30}} \: \\ $$$$=\:\mathrm{2}^{\mathrm{30}} \mathrm{5}^{\mathrm{40}} \:. \\ $$
Commented by rahul 19 last updated on 29/Nov/18
thank you sir!����
