
Question Number 114071 by bobhans last updated on 17/Sep/20
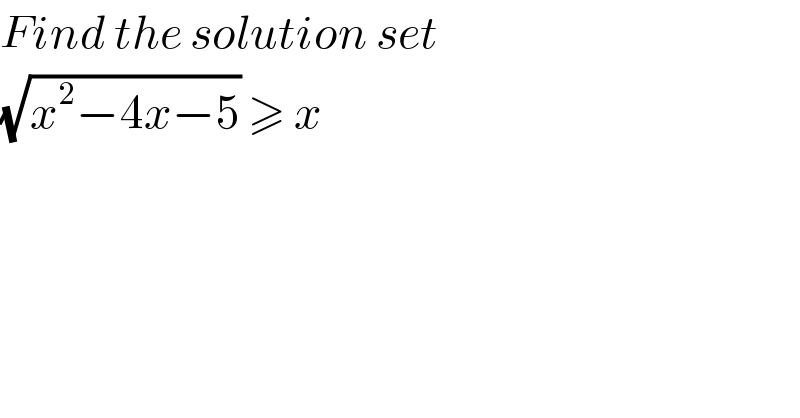
$${Find}\:{the}\:{solution}\:{set}\: \\ $$$$\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{5}}\:\geqslant\:{x} \\ $$
Commented by prakash jain last updated on 17/Sep/20

$$ \\ $$
Commented by bemath last updated on 17/Sep/20
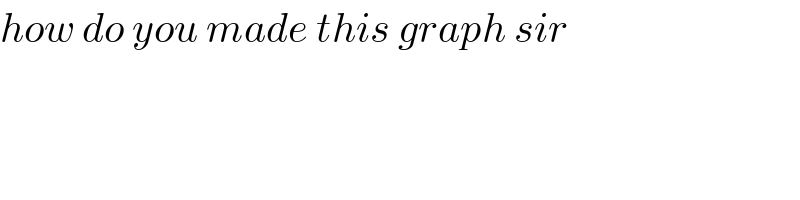
$${how}\:{do}\:{you}\:{made}\:{this}\:{graph}\:{sir} \\ $$
Commented by prakash jain last updated on 17/Sep/20

$$\mathrm{From}\:\mathrm{this}\:\mathrm{app}\:\mathrm{only},\:\mathrm{i}\:\mathrm{was}\:\mathrm{just} \\ $$$$\mathrm{checking} \\ $$$$\mathrm{steps}: \\ $$$${a}.\:\mathrm{insert}\:\mathrm{drawing} \\ $$$$\mathrm{b}.\:\mathrm{insert}\:\mathrm{equation}\:\mathrm{and}\:\mathrm{pasted}\:\mathrm{equation}\:\mathrm{1}. \\ $$$$\mathrm{c}.\:\mathrm{from}\:\mathrm{BUILD}\:\mathrm{menu}\:\mathrm{select}\:\mathrm{plot} \\ $$$$\mathrm{d}.\:\mathrm{repeated}\:\mathrm{procedure}\:\mathrm{for}\:\mathrm{other}\:\mathrm{equation}. \\ $$$$\mathrm{see}\:\mathrm{Q113542}. \\ $$
Commented by bemath last updated on 17/Sep/20

$${thank}\:{you}\:{sir} \\ $$
Answered by bemath last updated on 17/Sep/20
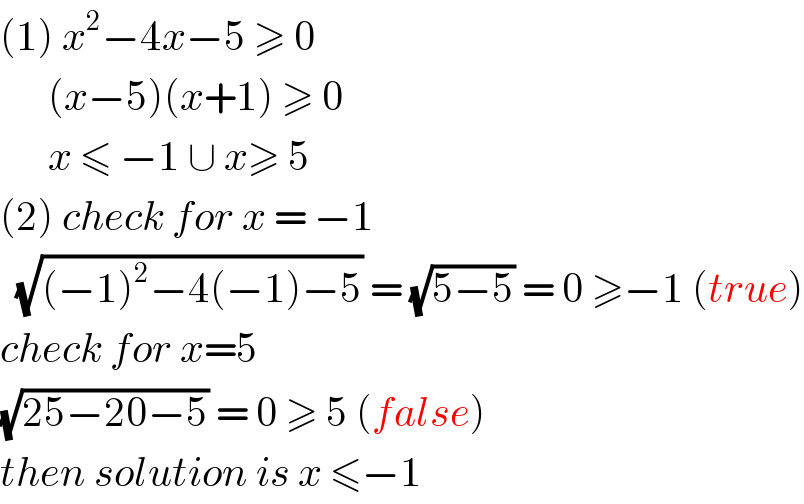
$$\left(\mathrm{1}\right)\:{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{5}\:\geqslant\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\left({x}−\mathrm{5}\right)\left({x}+\mathrm{1}\right)\:\geqslant\:\mathrm{0} \\ $$$$\:\:\:\:\:\:{x}\:\leqslant\:−\mathrm{1}\:\cup\:{x}\geqslant\:\mathrm{5} \\ $$$$\left(\mathrm{2}\right)\:{check}\:{for}\:{x}\:=\:−\mathrm{1} \\ $$$$\:\:\sqrt{\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left(−\mathrm{1}\right)−\mathrm{5}}\:=\:\sqrt{\mathrm{5}−\mathrm{5}}\:=\:\mathrm{0}\:\geqslant−\mathrm{1}\:\left({true}\right) \\ $$$${check}\:{for}\:{x}=\mathrm{5}\: \\ $$$$\sqrt{\mathrm{25}−\mathrm{20}−\mathrm{5}}\:=\:\mathrm{0}\:\geqslant\:\mathrm{5}\:\left({false}\right) \\ $$$${then}\:{solution}\:{is}\:{x}\:\leqslant−\mathrm{1} \\ $$
Commented by bemath last updated on 17/Sep/20

Commented by bobhans last updated on 17/Sep/20

$${santuyy} \\ $$
