
Previous in Differential Equation Next in Differential Equation
Question Number 2052 by Yozzi last updated on 01/Nov/15
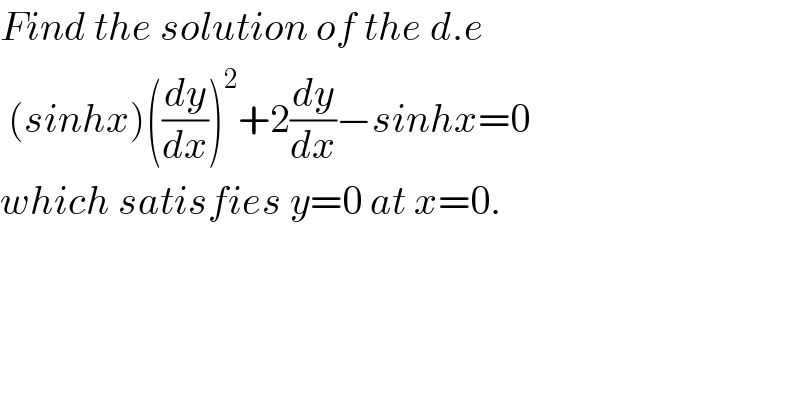
$${Find}\:{the}\:{solution}\:{of}\:{the}\:{d}.{e} \\ $$$$\:\left({sinhx}\right)\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} +\mathrm{2}\frac{{dy}}{{dx}}−{sinhx}=\mathrm{0} \\ $$$${which}\:{satisfies}\:{y}=\mathrm{0}\:{at}\:{x}=\mathrm{0}. \\ $$
Commented by prakash jain last updated on 01/Nov/15
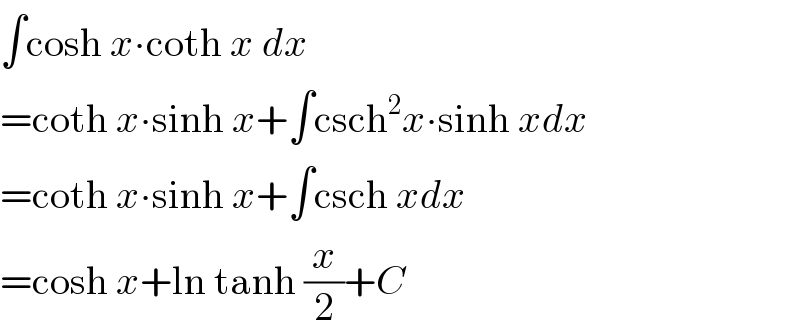
$$\int\mathrm{cosh}\:{x}\centerdot\mathrm{coth}\:{x}\:{dx} \\ $$$$=\mathrm{coth}\:{x}\centerdot\mathrm{sinh}\:{x}+\int\mathrm{csch}^{\mathrm{2}} {x}\centerdot\mathrm{sinh}\:{xdx} \\ $$$$=\mathrm{coth}\:{x}\centerdot\mathrm{sinh}\:{x}+\int\mathrm{csch}\:{xdx} \\ $$$$=\mathrm{cosh}\:{x}+\mathrm{ln}\:\mathrm{tanh}\:\frac{{x}}{\mathrm{2}}+{C} \\ $$
Commented by Rasheed Soomro last updated on 04/Nov/15
![Find the solution of the d.e (sinhx)((dy/dx))^2 +2(dy/dx)−sinhx=0 which satisfies y=0 at x=0. −−−−−−−−−−++++−−−−−−− Let (dy/dx)=u (sinh x)u^2 +2u−sinh x=0 u=((−2±(√((2)^2 −4(sinh x)(−sinh x))))/(2sinh x)) =((−2±2(√(1+sinh^2 x)))/(2sinh x)) =((−1±cosh x)/(sinh x)) u=((cosh x−1)/(sinh x)) ∣ u=−((1+cosh x)/(sinh x)) u=((cosh x)/(sinh x))−(1/(sinh x)) ∣ u=−((1+cosh x)/(sinh x)) (dy/dx)= coth x−csch x ∣ (dy/dx)=−(1/(sinh x))−((cosh x)/(sinh x)) y=∫( coth x−csch x)dx ∣ y=−∫(csch x+coth x)dx y=∫( coth x)dx−∫(csch x)dx ∣ y=−∫(csch x)dx−∫(coth x)dx =ln∣sinh x∣−ln∣tanh(x/2)∣+C_(−) ∣ =−ln∣sinh x∣−ln∣tanh(x/2)∣+C Further evaluation Suggested by Mr. Yozzi: y=ln((sinh x)/(tanh (x/2)))+C ∣y=−ln∣(sinh x)(tanh(x/2))∣+C y=ln{2sinh(x/2)cosh(x/2)×((cosh (x/2))/(sinh(x/2)))}+C∣y=−ln{2sinh(x/2)cosh(x/2)×((sinh (x/2))/(cosh(x/2)))}+C =ln{2cosh^2 (x/2)}+C ∣ y=−ln{2sinh^2 (x/2)}+C [C is not defined] See comment (02−11−2015) by Yozzi for further process.](Q2058.png)
$$ \\ $$$${Find}\:{the}\:{solution}\:{of}\:{the}\:{d}.{e} \\ $$$$\left({sinhx}\right)\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} +\mathrm{2}\frac{{dy}}{{dx}}−{sinhx}=\mathrm{0} \\ $$$${which}\:{satisfies}\:{y}=\mathrm{0}\:{at}\:{x}=\mathrm{0}. \\ $$$$−−−−−−−−−−++++−−−−−−− \\ $$$${Let}\:\:\frac{{dy}}{{dx}}={u} \\ $$$$\left({sinh}\:{x}\right){u}^{\mathrm{2}} +\mathrm{2}{u}−{sinh}\:{x}=\mathrm{0} \\ $$$${u}=\frac{−\mathrm{2}\pm\sqrt{\left(\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}\left({sinh}\:{x}\right)\left(−{sinh}\:{x}\right)}}{\mathrm{2}{sinh}\:{x}} \\ $$$$\:\:\:=\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{1}+{sinh}^{\mathrm{2}} {x}}}{\mathrm{2}{sinh}\:{x}} \\ $$$$\:\:\:=\frac{−\mathrm{1}\pm{cosh}\:{x}}{{sinh}\:{x}} \\ $$$$\:\:\:\:\:{u}=\frac{{cosh}\:{x}−\mathrm{1}}{{sinh}\:{x}}\:\mid\:{u}=−\frac{\mathrm{1}+{cosh}\:{x}}{{sinh}\:{x}} \\ $$$${u}=\frac{{cosh}\:{x}}{{sinh}\:{x}}−\frac{\mathrm{1}}{{sinh}\:{x}}\:\:\:\mid\:{u}=−\frac{\mathrm{1}+{cosh}\:{x}}{{sinh}\:{x}} \\ $$$$\frac{{dy}}{{dx}}=\:{coth}\:{x}−{csch}\:{x}\:\:\mid\:\frac{{dy}}{{dx}}=−\frac{\mathrm{1}}{{sinh}\:{x}}−\frac{{cosh}\:{x}}{{sinh}\:{x}} \\ $$$${y}=\int\left(\:{coth}\:{x}−{csch}\:{x}\right){dx}\:\mid\:{y}=−\int\left({csch}\:{x}+{coth}\:{x}\right){dx} \\ $$$${y}=\int\left(\:{coth}\:{x}\right){dx}−\int\left({csch}\:{x}\right){dx}\:\mid\:{y}=−\int\left({csch}\:{x}\right){dx}−\int\left({coth}\:{x}\right){dx} \\ $$$$\:\underset{−} {\:\:={ln}\mid{sinh}\:{x}\mid−{ln}\mid{tanh}\frac{{x}}{\mathrm{2}}\mid+{C}}\:\mid\:=−{ln}\mid{sinh}\:{x}\mid−{ln}\mid{tanh}\frac{{x}}{\mathrm{2}}\mid+{C} \\ $$$${Further}\:{evaluation}\: \\ $$$${Suggested}\:{by}\:{Mr}.\:{Yozzi}: \\ $$$${y}={ln}\frac{{sinh}\:{x}}{{tanh}\:\frac{{x}}{\mathrm{2}}}+{C}\:\mid{y}=−{ln}\mid\left({sinh}\:{x}\right)\left({tanh}\frac{{x}}{\mathrm{2}}\right)\mid+{C} \\ $$$${y}={ln}\left\{\mathrm{2}{sinh}\frac{{x}}{\mathrm{2}}{cosh}\frac{{x}}{\mathrm{2}}×\frac{{cosh}\:\frac{{x}}{\mathrm{2}}}{{sinh}\frac{{x}}{\mathrm{2}}}\right\}+{C}\mid{y}=−{ln}\left\{\mathrm{2}{sinh}\frac{{x}}{\mathrm{2}}{cosh}\frac{{x}}{\mathrm{2}}×\frac{{sinh}\:\frac{{x}}{\mathrm{2}}}{{cosh}\frac{{x}}{\mathrm{2}}}\right\}+{C} \\ $$$$\:\:={ln}\left\{\mathrm{2}{cosh}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right\}+{C}\:\:\mid\:{y}=−{ln}\left\{\mathrm{2}{sinh}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right\}+{C}\:\left[{C}\:{is}\:{not}\:{defined}\right] \\ $$$$\:\: \\ $$$${See}\:{comment}\:\left(\mathrm{02}−\mathrm{11}−\mathrm{2015}\right)\:{by}\:{Yozzi}\:{for}\:{further}\:{process}. \\ $$
Commented by Yozzi last updated on 01/Nov/15

$${There}'{s}\:{an}\:{error}\:{in}\:{your}\:{evaluation}\:{Mr}.\:{Soomro}. \\ $$$$\sqrt{\mathrm{1}+{sinh}^{\mathrm{2}} {x}}=\pm{coshx}\neq{cosh}^{\mathrm{2}} {x}. \\ $$$${I}\:{appreciate}\:{the}\:{integral} \\ $$$$\int{coshxcothxdx}\:{that}\:{arose}\:{however}. \\ $$$${Errors}\:{could}\:{lead}\:{one}\:{to}\:{learning}\:{new} \\ $$$${things}. \\ $$
Commented by Rasheed Soomro last updated on 03/Nov/15
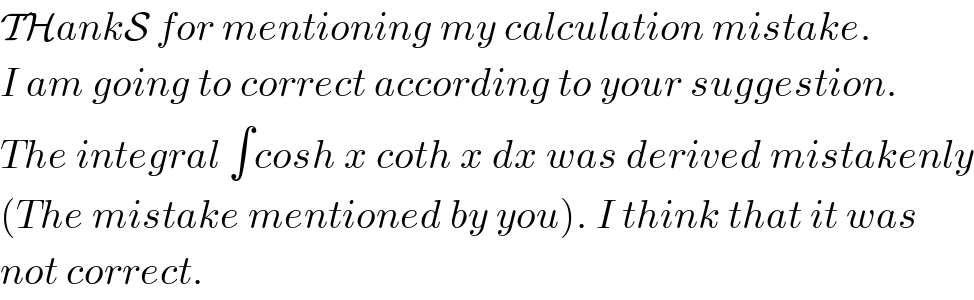
$$\mathcal{TH}{ank}\mathcal{S}\:{for}\:{mentioning}\:{my}\:{calculation}\:{mistake}. \\ $$$${I}\:{am}\:{going}\:{to}\:{correct}\:{according}\:{to}\:{your}\:{suggestion}. \\ $$$${The}\:{integral}\:\int{cosh}\:{x}\:{coth}\:{x}\:{dx}\:{was}\:{derived}\:{mistakenly} \\ $$$$\left({The}\:{mistake}\:{mentioned}\:{by}\:{you}\right).\:{I}\:{think}\:{that}\:{it}\:{was} \\ $$$${not}\:{correct}. \\ $$
Commented by Yozzi last updated on 02/Nov/15

$${If}\:{you}\:{go}\:{further}\:{on}\:{simplifying} \\ $$$${the}\:{first}\:{answer}\:{you}\:{get} \\ $$$${y}={ln}\mid\frac{{sinhx}}{{tanh}\frac{{x}}{\mathrm{2}}}\mid+{C} \\ $$$${y}={ln}\mid\mathrm{2}{cosh}\frac{{x}}{\mathrm{2}}{sinh}\frac{{x}}{\mathrm{2}}×\frac{{cosh}\left({x}/\mathrm{2}\right)}{{sinh}\left({x}/\mathrm{2}\right)}\mid+{C} \\ $$$${y}={ln}\mid\mathrm{2}{cosh}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\mid+{C} \\ $$$${y}=\mathrm{0}\:{at}\:{x}=\mathrm{0} \\ $$$$\therefore\:{C}=−{ln}\mathrm{2} \\ $$$$\therefore{y}={ln}\mid\mathrm{2}{cosh}^{\mathrm{2}} \mathrm{0}.\mathrm{5}{x}\mid−{ln}\mathrm{2} \\ $$$${y}={ln}\mid\frac{\mathrm{2}}{\mathrm{2}}{cosh}^{\mathrm{2}} \mathrm{0}.\mathrm{5}{x}\mid \\ $$$${y}={ln}\mid{cosh}^{\mathrm{2}} \mathrm{0}.\mathrm{5}{x}\mid \\ $$$${y}=\mathrm{2}{ln}\mid{cosh}\mathrm{0}.\mathrm{5}{x}\mid \\ $$$${coshx}>\mathrm{0}\:\forall{x}\in\mathbb{R} \\ $$$$\therefore{y}=\mathrm{2}{lncosh}\mathrm{0}.\mathrm{5}{x}. \\ $$$${The}\:{second}\:{solution}\:{turns}\:{out}\:{not} \\ $$$${to}\:{be}\:{a}\:{solution}. \\ $$$${Checking}\:{y}=\mathrm{2}{lncosh}\mathrm{0}.\mathrm{5}{x}. \\ $$$${y}^{'} =\mathrm{2}×\frac{\mathrm{0}.\mathrm{5}{sinh}\mathrm{0}.\mathrm{5}{x}}{{cosh}\mathrm{0}.\mathrm{5}{x}}={tanh}\mathrm{0}.\mathrm{5}{x} \\ $$$$\left({y}^{'} \overset{\mathrm{2}} {\right)}={tanh}^{\mathrm{2}} \mathrm{0}.\mathrm{5}{x} \\ $$$${sinhxtanh}^{\mathrm{2}} \mathrm{0}.\mathrm{5}{x}+\mathrm{2}{tanh}\mathrm{0}.\mathrm{5}{x}−{sinhx} \\ $$$$={sinhx}\left(−{sech}^{\mathrm{2}} \mathrm{0}.\mathrm{5}{x}\right)+\mathrm{2}{tanh}\mathrm{0}.\mathrm{5}{x} \\ $$$$=\frac{\mathrm{2}{sinh}\mathrm{0}.\mathrm{5}{xcosh}\mathrm{0}.\mathrm{5}{x}}{−{cosh}^{\mathrm{2}} \mathrm{0}.\mathrm{5}{x}}+\mathrm{2}{tanh}\mathrm{0}.\mathrm{5}{x} \\ $$$$=−\mathrm{2}{tanh}\mathrm{0}.\mathrm{5}{x}+\mathrm{2}{tanh}\mathrm{0}.\mathrm{5}{x} \\ $$$$=\mathrm{0}\:{as}\:{required}. \\ $$$$ \\ $$$${The}\:{other}\:{solution}\:{is}\:{invalid}\:{however}. \\ $$$${since}\:{ln}\mathrm{0}\:{is}\:{undefined}.\: \\ $$
