
Question Number 28198 by NECx last updated on 21/Jan/18
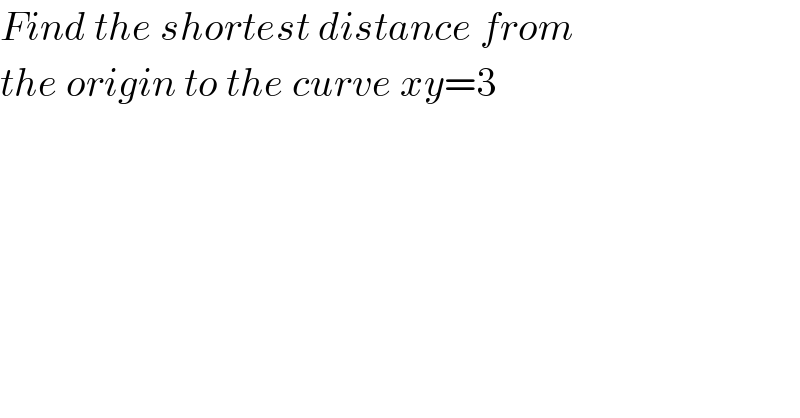
$${Find}\:{the}\:{shortest}\:{distance}\:{from} \\ $$$${the}\:{origin}\:{to}\:{the}\:{curve}\:{xy}=\mathrm{3} \\ $$
Answered by mrW2 last updated on 22/Jan/18
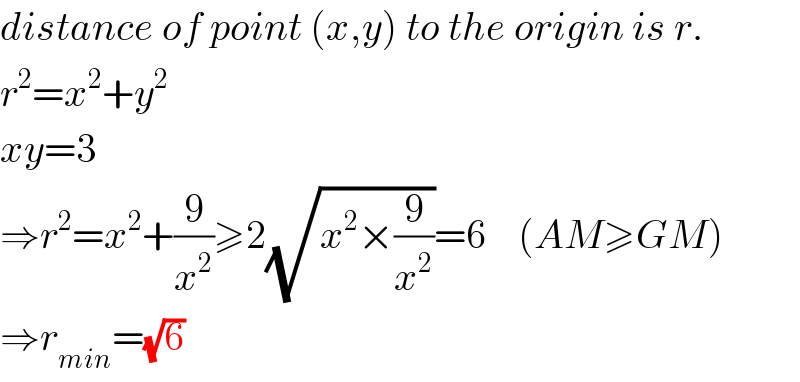
$${distance}\:{of}\:{point}\:\left({x},{y}\right)\:{to}\:{the}\:{origin}\:{is}\:{r}. \\ $$$${r}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${xy}=\mathrm{3} \\ $$$$\Rightarrow{r}^{\mathrm{2}} ={x}^{\mathrm{2}} +\frac{\mathrm{9}}{{x}^{\mathrm{2}} }\geqslant\mathrm{2}\sqrt{{x}^{\mathrm{2}} ×\frac{\mathrm{9}}{{x}^{\mathrm{2}} }}=\mathrm{6}\:\:\:\:\left({AM}\geqslant{GM}\right) \\ $$$$\Rightarrow{r}_{{min}} =\sqrt{\mathrm{6}} \\ $$
Commented by math solver last updated on 22/Jan/18

$${nice}\:! \\ $$
