
Question Number 56697 by Tawa1 last updated on 21/Mar/19
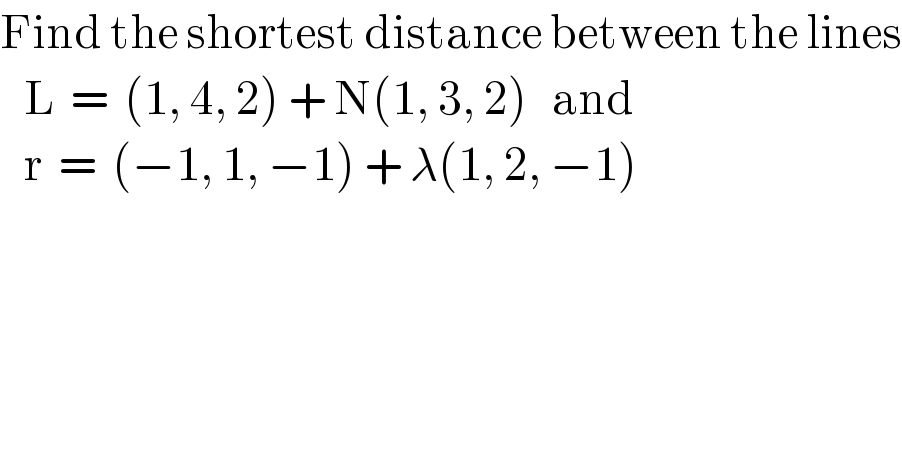
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{shortest}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{the}\:\mathrm{lines} \\ $$$$\:\:\:\mathrm{L}\:\:=\:\:\left(\mathrm{1},\:\mathrm{4},\:\mathrm{2}\right)\:+\:\mathrm{N}\left(\mathrm{1},\:\mathrm{3},\:\mathrm{2}\right)\:\:\:\mathrm{and} \\ $$$$\:\:\:\mathrm{r}\:\:=\:\:\left(−\mathrm{1},\:\mathrm{1},\:−\mathrm{1}\right)\:+\:\lambda\left(\mathrm{1},\:\mathrm{2},\:−\mathrm{1}\right) \\ $$
Answered by mr W last updated on 21/Mar/19
![many methods to solve. d^2 =[1+N−(−1+λ)]^2 +[4+3N−(1+2λ)]^2 +[2+2N−(−1−λ)]^2 d^2 =(2+N−λ)^2 +(3+3N−2λ)^2 +(3+2N+λ)^2 ...(iii) ((∂(d^2 ))/∂N)=2(2+N−λ)+2×3(3+3N−2λ)+2×2(3+2N+λ)=0 ⇒14N−5λ+17=0 ...(i) ((∂(d^2 ))/∂λ)=−2(2+N−λ)−2×2(3+3N−2λ)+2(3+2N+λ)=0 ⇒5N−6λ+5=0 ...(ii) solve (i) and (ii): ⇒N=−((77)/(59)) ⇒λ=−((15)/(59)) put this into (iii): d_(min) ^2 =(((56)/(59)))^2 +(((−24)/(59)))^2 +((8/(59)))^2 ⇒d_(min) =((√(56^2 +24^2 +8^2 ))/(59))=(8/(√(59)))=1.0415](Q56701.png)
$${many}\:{methods}\:{to}\:{solve}. \\ $$$$ \\ $$$${d}^{\mathrm{2}} =\left[\mathrm{1}+{N}−\left(−\mathrm{1}+\lambda\right)\right]^{\mathrm{2}} +\left[\mathrm{4}+\mathrm{3}{N}−\left(\mathrm{1}+\mathrm{2}\lambda\right)\right]^{\mathrm{2}} +\left[\mathrm{2}+\mathrm{2}{N}−\left(−\mathrm{1}−\lambda\right)\right]^{\mathrm{2}} \\ $$$${d}^{\mathrm{2}} =\left(\mathrm{2}+{N}−\lambda\right)^{\mathrm{2}} +\left(\mathrm{3}+\mathrm{3}{N}−\mathrm{2}\lambda\right)^{\mathrm{2}} +\left(\mathrm{3}+\mathrm{2}{N}+\lambda\right)^{\mathrm{2}} \:\:\:...\left({iii}\right) \\ $$$$\frac{\partial\left({d}^{\mathrm{2}} \right)}{\partial{N}}=\mathrm{2}\left(\mathrm{2}+{N}−\lambda\right)+\mathrm{2}×\mathrm{3}\left(\mathrm{3}+\mathrm{3}{N}−\mathrm{2}\lambda\right)+\mathrm{2}×\mathrm{2}\left(\mathrm{3}+\mathrm{2}{N}+\lambda\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{14}{N}−\mathrm{5}\lambda+\mathrm{17}=\mathrm{0}\:\:\:...\left({i}\right) \\ $$$$\frac{\partial\left({d}^{\mathrm{2}} \right)}{\partial\lambda}=−\mathrm{2}\left(\mathrm{2}+{N}−\lambda\right)−\mathrm{2}×\mathrm{2}\left(\mathrm{3}+\mathrm{3}{N}−\mathrm{2}\lambda\right)+\mathrm{2}\left(\mathrm{3}+\mathrm{2}{N}+\lambda\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{5}{N}−\mathrm{6}\lambda+\mathrm{5}=\mathrm{0}\:\:\:...\left({ii}\right) \\ $$$$ \\ $$$${solve}\:\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$$\Rightarrow{N}=−\frac{\mathrm{77}}{\mathrm{59}} \\ $$$$\Rightarrow\lambda=−\frac{\mathrm{15}}{\mathrm{59}} \\ $$$$ \\ $$$${put}\:{this}\:{into}\:\left({iii}\right): \\ $$$${d}_{{min}} ^{\mathrm{2}} =\left(\frac{\mathrm{56}}{\mathrm{59}}\right)^{\mathrm{2}} +\left(\frac{−\mathrm{24}}{\mathrm{59}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{8}}{\mathrm{59}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{d}_{{min}} =\frac{\sqrt{\mathrm{56}^{\mathrm{2}} +\mathrm{24}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} }}{\mathrm{59}}=\frac{\mathrm{8}}{\sqrt{\mathrm{59}}}=\mathrm{1}.\mathrm{0415} \\ $$
Commented by Tawa1 last updated on 22/Mar/19
$$\mathrm{Wow},\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\: \\ $$
Answered by mr W last updated on 23/Mar/19

$${vector}\:{method} \\ $$$$ \\ $$$${normal}\:{to}\:{L}\:{and}\:{r}: \\ $$$$\left(\mathrm{1},\mathrm{3},\mathrm{2}\right)×\left(\mathrm{1},\mathrm{2},−\mathrm{1}\right)=\left(−\mathrm{7},\mathrm{3},−\mathrm{1}\right) \\ $$$$ \\ $$$$\left(\mathrm{1}+\mathrm{1},\mathrm{4}−\mathrm{1},\mathrm{2}+\mathrm{1}\right)=\left(\mathrm{2},\mathrm{3},\mathrm{3}\right) \\ $$$$ \\ $$$$\left(\mathrm{2},\mathrm{3},\mathrm{3}\right)\bullet\left(−\mathrm{7},\mathrm{3},−\mathrm{1}\right)=−\mathrm{14}+\mathrm{9}−\mathrm{3}=−\mathrm{8} \\ $$$$ \\ $$$${d}=\frac{\mid−\mathrm{8}\mid}{\sqrt{\left(−\mathrm{7}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\left(−\mathrm{1}\right)^{\mathrm{2}} }}=\frac{\mathrm{8}}{\sqrt{\mathrm{59}}}\approx\mathrm{1}.\mathrm{0415} \\ $$
Commented by Tawa1 last updated on 24/Mar/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
