
Question Number 52573 by Necxx last updated on 09/Jan/19

$${Find}\:{the}\:{relation}\:{between}\:{p}\:{q}\:{and}\:{r} \\ $$$${if}\:{one}\:{of}\:{the}\:{root}\:{of}\:{the}\:{equation} \\ $$$${px}^{\mathrm{2}} +{qx}+{r}=\mathrm{0}\:{is}\:{double}\:{the}\:{other}. \\ $$
Answered by mr W last updated on 09/Jan/19
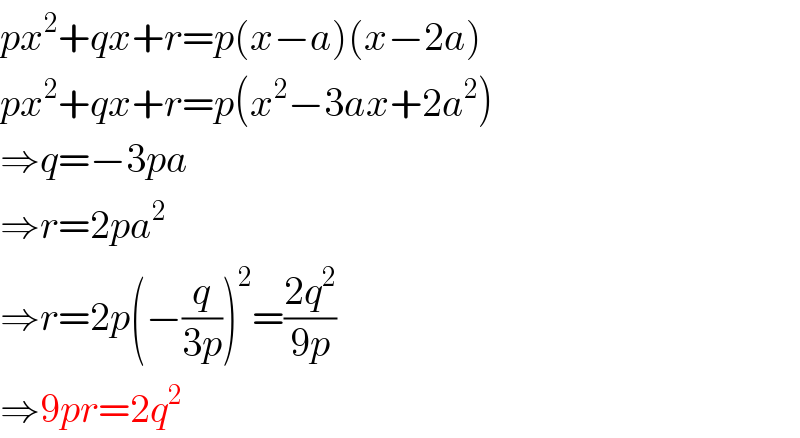
$${px}^{\mathrm{2}} +{qx}+{r}={p}\left({x}−{a}\right)\left({x}−\mathrm{2}{a}\right) \\ $$$${px}^{\mathrm{2}} +{qx}+{r}={p}\left({x}^{\mathrm{2}} −\mathrm{3}{ax}+\mathrm{2}{a}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{q}=−\mathrm{3}{pa} \\ $$$$\Rightarrow{r}=\mathrm{2}{pa}^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\mathrm{2}{p}\left(−\frac{{q}}{\mathrm{3}{p}}\right)^{\mathrm{2}} =\frac{\mathrm{2}{q}^{\mathrm{2}} }{\mathrm{9}{p}} \\ $$$$\Rightarrow\mathrm{9}{pr}=\mathrm{2}{q}^{\mathrm{2}} \\ $$
Commented by Necxx last updated on 10/Jan/19

$${thank}\:{you}\:{sir} \\ $$
