
Question Number 207450 by York12 last updated on 15/May/24
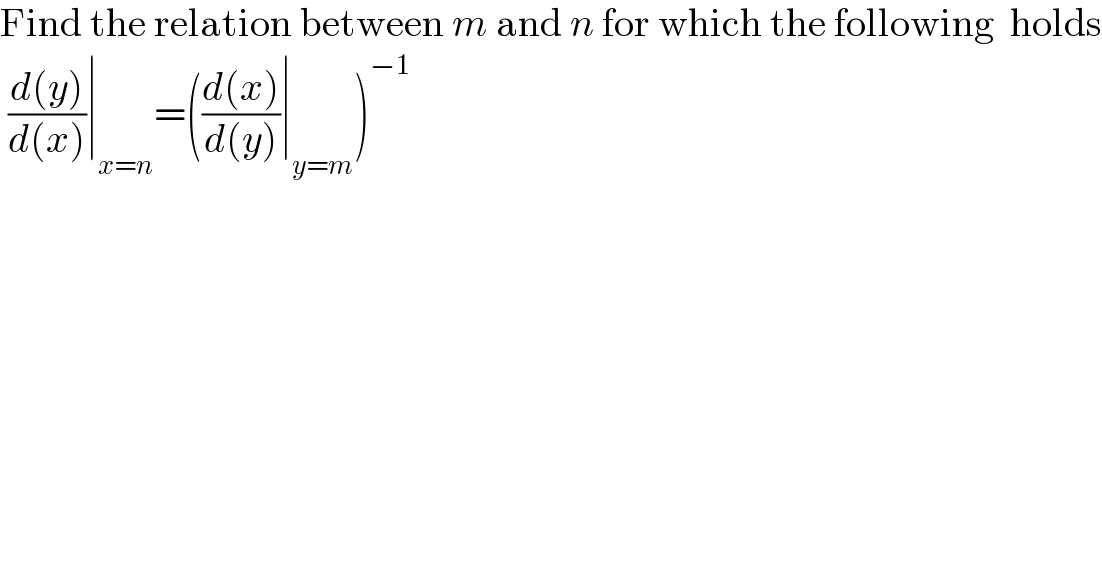
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{relation}\:\mathrm{between}\:{m}\:\mathrm{and}\:{n}\:\mathrm{for}\:\mathrm{which}\:\mathrm{the}\:\mathrm{following}\:\:\mathrm{holds} \\ $$$$\:\frac{{d}\left({y}\right)}{{d}\left({x}\right)}\mid_{{x}={n}} =\left(\frac{{d}\left({x}\right)}{{d}\left({y}\right)}\mid_{{y}={m}} \right)^{−\mathrm{1}} \\ $$
Answered by mr W last updated on 15/May/24
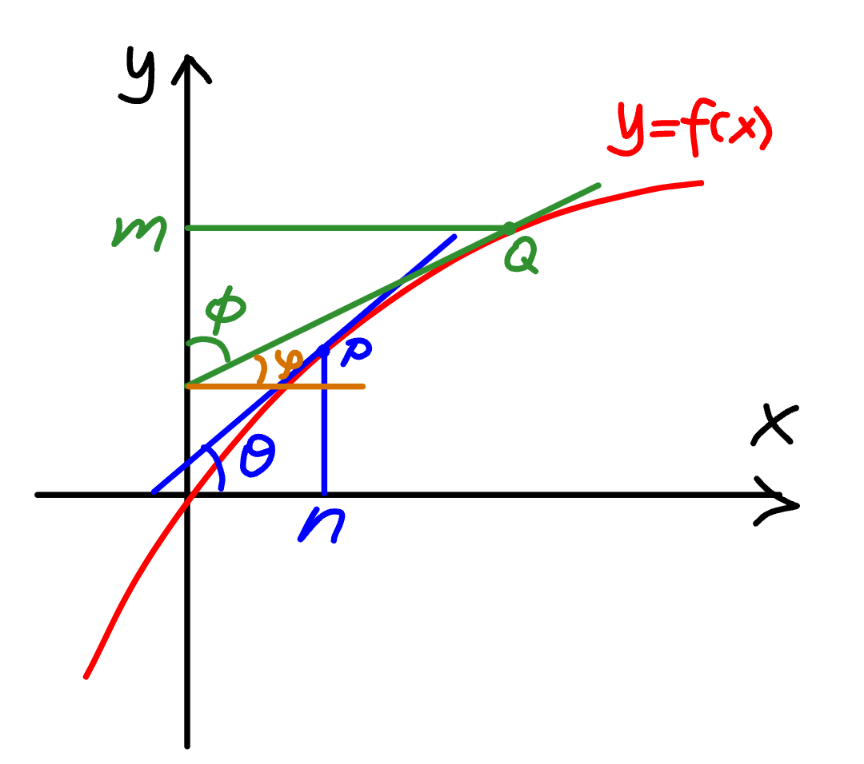
Commented by mr W last updated on 15/May/24

$$\frac{{dy}}{{dx}}\mid_{{x}={n}} =\mathrm{tan}\:\theta \\ $$$$\frac{{dx}}{{dy}}\mid_{{y}={m}} =\mathrm{tan}\:\phi \\ $$$$\left(\frac{{dx}}{{dy}}\mid_{{y}={m}} \right)^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{tan}\:\phi}=\mathrm{tan}\:\varphi \\ $$$$\frac{{dy}}{{dx}}\mid_{{x}={n}} =\left(\frac{{dx}}{{dy}}\mid_{{y}={m}} \right)^{−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\mathrm{tan}\:\varphi \\ $$$$\Rightarrow\theta=\varphi \\ $$$${if}\:{y}={f}\left({x}\right)\:{is}\:{a}\:{strictly}\:{monotonic} \\ $$$${function},\:{then}\:{P}\:\:{and}\:{Q}\:{must}\:{be} \\ $$$${the}\:{same}\:{point},\:{i}.{e}.\:\:{m}={f}\left({n}\right). \\ $$$${if}\:{y}={f}\left({x}\right)\:{is}\:{not}\:{a}\:{strictly}\:{monotonic} \\ $$$${function},\:{then}\:{the}\:{relation}\:{between} \\ $$$${n}\:{und}\:{m}\:{is}\:{not}\:{unique}. \\ $$
Commented by York12 last updated on 15/May/24

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
