
Question Number 184873 by topgrace100 last updated on 13/Jan/23
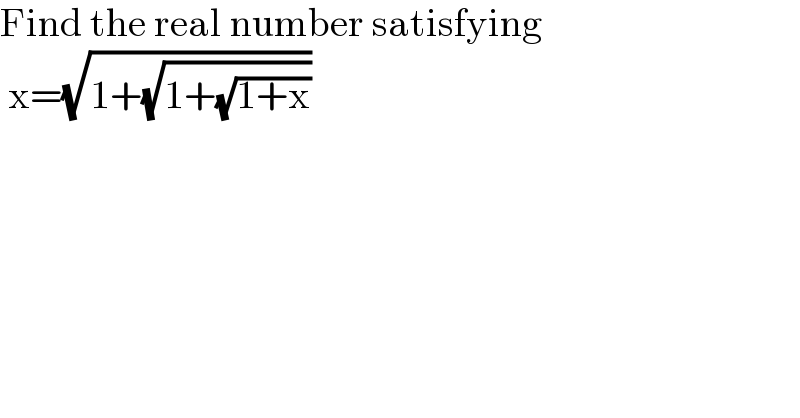
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{real}\:\mathrm{number}\:\mathrm{satisfying} \\ $$$$\:\mathrm{x}=\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{x}}}} \\ $$
Answered by Rasheed.Sindhi last updated on 13/Jan/23
![x=(√(1+(√(1+(√(1+x)))))) x=(√(1+(√(1+(√(1+(√(1+(√(1+...)))))))))) x^2 =1+x x^2 −x−1=0 x=((1+(√(1+4)))/2)=((1+(√5))/2) ✓[∵((1−(√(5 )) )/2)<0 ]](Q184874.png)
$$\:\mathrm{x}=\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{x}}}} \\ $$$$\:\mathrm{x}=\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+...}}}}} \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{1}+\mathrm{x} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{x}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\checkmark\left[\because\frac{\mathrm{1}−\sqrt{\mathrm{5}\:}\:}{\mathrm{2}}<\mathrm{0}\:\right] \\ $$
Commented by Frix last updated on 13/Jan/23
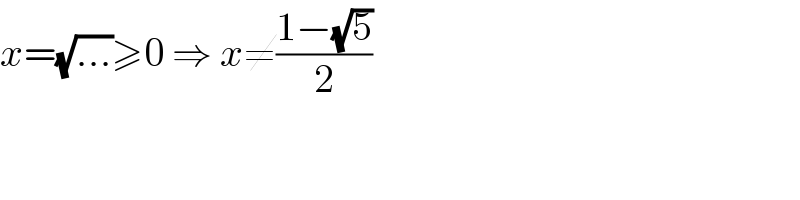
$${x}=\sqrt{...}\geqslant\mathrm{0}\:\Rightarrow\:{x}\neq\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 13/Jan/23
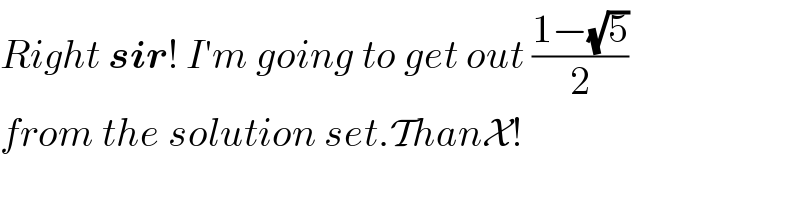
$${Right}\:\boldsymbol{{sir}}!\:{I}'{m}\:{going}\:{to}\:{get}\:{out}\:\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${from}\:{the}\:{solution}\:{set}.\mathcal{T}{han}\mathcal{X}! \\ $$
