
Previous in Differential Equation Next in Differential Equation
Question Number 193733 by Tawa11 last updated on 18/Jun/23
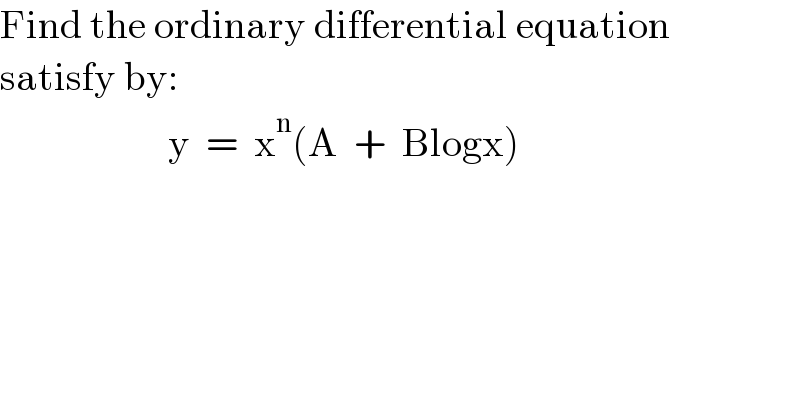
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{ordinary}\:\mathrm{differential}\:\mathrm{equation} \\ $$$$\mathrm{satisfy}\:\mathrm{by}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{y}\:\:=\:\:\mathrm{x}^{\mathrm{n}} \left(\mathrm{A}\:\:+\:\:\mathrm{Blogx}\right) \\ $$
Answered by Rajpurohith last updated on 19/Jun/23
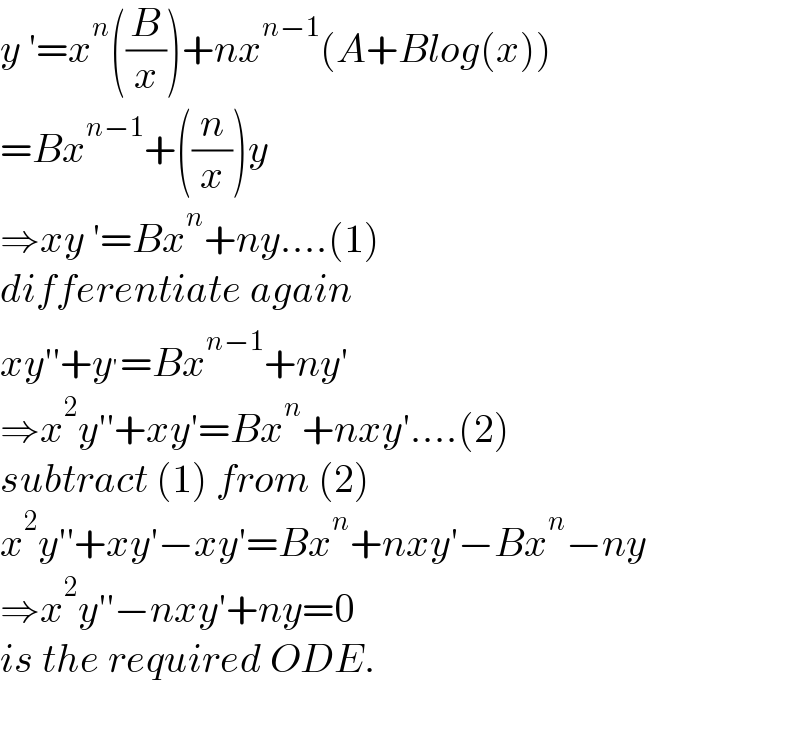
$${y}\:'={x}^{{n}} \left(\frac{{B}}{{x}}\right)+{nx}^{{n}−\mathrm{1}} \left({A}+{Blog}\left({x}\right)\right) \\ $$$$={Bx}^{{n}−\mathrm{1}} +\left(\frac{{n}}{{x}}\right){y} \\ $$$$\Rightarrow{xy}\:'={Bx}^{{n}} +{ny}....\left(\mathrm{1}\right) \\ $$$${differentiate}\:{again} \\ $$$${xy}''+{y}^{'} ={Bx}^{{n}−\mathrm{1}} +{ny}' \\ $$$$\Rightarrow{x}^{\mathrm{2}} {y}''+{xy}'={Bx}^{{n}} +{nxy}'....\left(\mathrm{2}\right) \\ $$$${subtract}\:\left(\mathrm{1}\right)\:{from}\:\left(\mathrm{2}\right) \\ $$$${x}^{\mathrm{2}} {y}''+{xy}'−{xy}'={Bx}^{{n}} +{nxy}'−{Bx}^{{n}} −{ny} \\ $$$$\Rightarrow{x}^{\mathrm{2}} {y}''−{nxy}'+{ny}=\mathrm{0} \\ $$$${is}\:{the}\:{required}\:{ODE}. \\ $$$$ \\ $$
Commented by Tawa11 last updated on 19/Jun/23

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
