
Question Number 215958 by Tawa11 last updated on 22/Jan/25
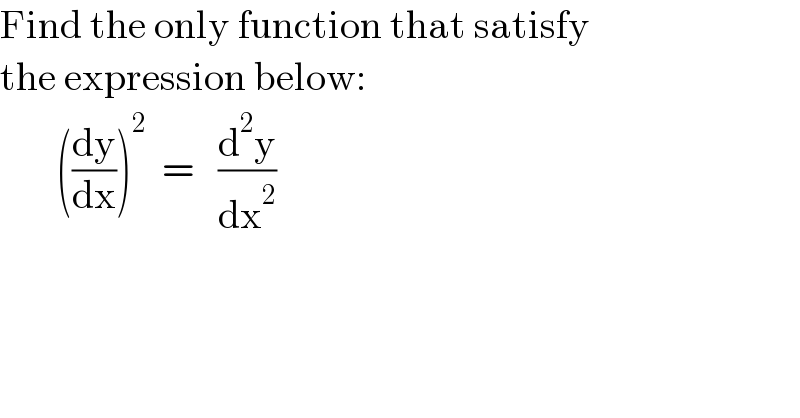
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{only}\:\mathrm{function}\:\mathrm{that}\:\mathrm{satisfy} \\ $$$$\mathrm{the}\:\mathrm{expression}\:\mathrm{below}: \\ $$$$\:\:\:\:\:\:\:\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} \:\:=\:\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} } \\ $$
Answered by Ghisom last updated on 23/Jan/25
![(y′)^2 =y′′ u=y′ u^2 =u′ u=−(1/(x+C_1 )) [from experience] u′=(1/((x+C_1 )^2 ))=u^2 y′=−(1/(x+C_1 )) ⇒ <y=−∫(dx/(x+C_1 ))=C_2 −ln ∣x+C_1 ∣](Q215962.png)
$$\left({y}'\right)^{\mathrm{2}} ={y}'' \\ $$$${u}={y}' \\ $$$${u}^{\mathrm{2}} ={u}' \\ $$$${u}=−\frac{\mathrm{1}}{{x}+{C}_{\mathrm{1}} }\:\:\:\:\:\left[\mathrm{from}\:\mathrm{experience}\right] \\ $$$${u}'=\frac{\mathrm{1}}{\left({x}+{C}_{\mathrm{1}} \right)^{\mathrm{2}} }={u}^{\mathrm{2}} \\ $$$${y}'=−\frac{\mathrm{1}}{{x}+{C}_{\mathrm{1}} }\:\Rightarrow \\ $$$$<{y}=−\int\frac{{dx}}{{x}+{C}_{\mathrm{1}} }={C}_{\mathrm{2}} −\mathrm{ln}\:\mid{x}+{C}_{\mathrm{1}} \mid \\ $$
Commented by Tawa11 last updated on 03/Feb/25
$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{apprecuate}. \\ $$
Answered by mr W last updated on 25/Jan/25
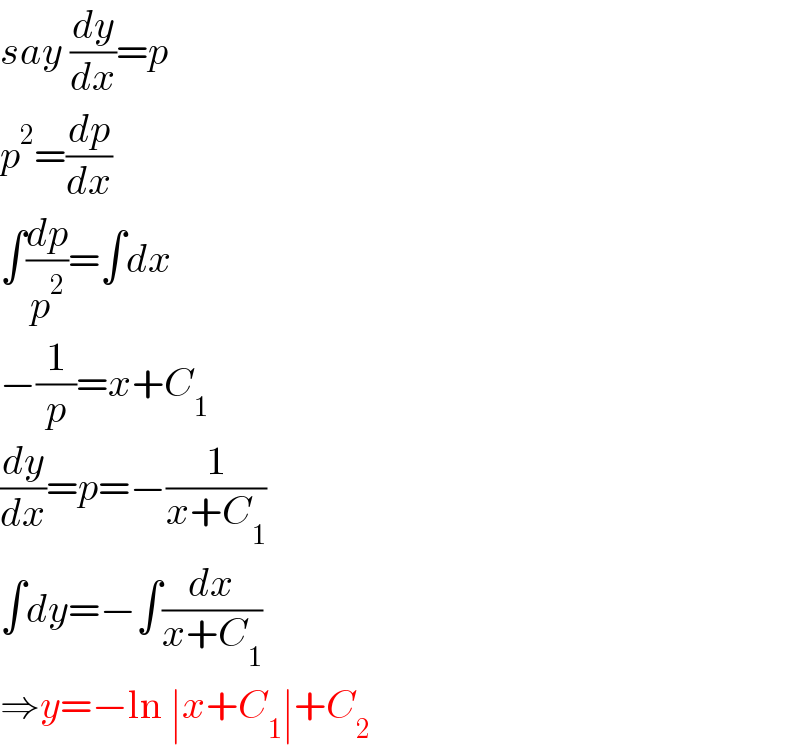
$${say}\:\frac{{dy}}{{dx}}={p} \\ $$$${p}^{\mathrm{2}} =\frac{{dp}}{{dx}} \\ $$$$\int\frac{{dp}}{{p}^{\mathrm{2}} }=\int{dx} \\ $$$$−\frac{\mathrm{1}}{{p}}={x}+{C}_{\mathrm{1}} \\ $$$$\frac{{dy}}{{dx}}={p}=−\frac{\mathrm{1}}{{x}+{C}_{\mathrm{1}} } \\ $$$$\int{dy}=−\int\frac{{dx}}{{x}+{C}_{\mathrm{1}} } \\ $$$$\Rightarrow{y}=−\mathrm{ln}\:\mid{x}+{C}_{\mathrm{1}} \mid+{C}_{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 03/Feb/25
$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$
