
Question Number 182474 by Acem last updated on 10/Dec/22
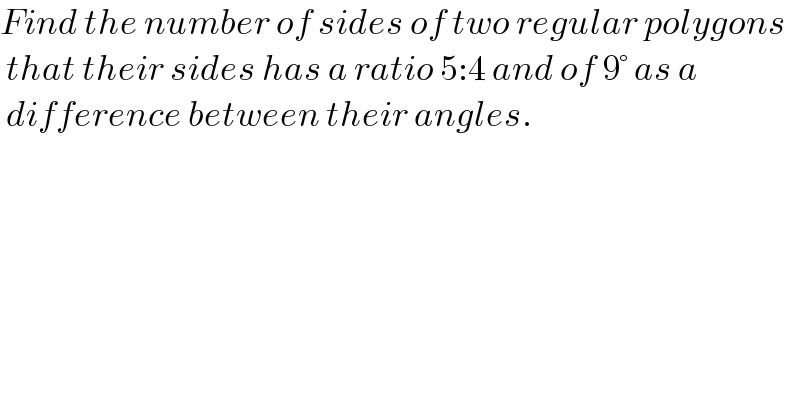
$${Find}\:{the}\:{number}\:{of}\:{sides}\:{of}\:{two}\:{regular}\:{polygons} \\ $$$$\:{that}\:{their}\:{sides}\:{has}\:{a}\:{ratio}\:\mathrm{5}:\mathrm{4}\:{and}\:{of}\:\mathrm{9}°\:{as}\:{a} \\ $$$$\:{difference}\:{between}\:{their}\:{angles}. \\ $$
Answered by mr W last updated on 10/Dec/22

$${n}−{sided}\:{regular}\:{polygon}: \\ $$$${angle}\:\theta_{{n}} =\mathrm{180}−\frac{\mathrm{360}}{{n}} \\ $$$${say}\:{two}\:{regular}\:{polygons}\:{with}\:{x}\:{and} \\ $$$${y}\:{sides}\:{respectively}. \\ $$$$\frac{{x}}{{y}}=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\theta_{{x}} −\theta_{{y}} =\frac{\mathrm{360}}{{y}}−\frac{\mathrm{360}}{{x}}=\mathrm{9} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{y}}−\frac{\mathrm{1}}{{x}}=\frac{\mathrm{1}}{\mathrm{40}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{y}}−\frac{\mathrm{4}}{\mathrm{5}{y}}=\frac{\mathrm{1}}{\mathrm{40}}\:\Rightarrow{y}=\mathrm{8}\:\Rightarrow{x}=\mathrm{10} \\ $$$${i}.{e}.\:{their}\:{number}\:{of}\:{sides}\:{is}\:\mathrm{10}\:{and}\:\mathrm{8} \\ $$$${respectively}. \\ $$
Commented by Acem last updated on 10/Dec/22

$${Thanks}\:{Sir}! \\ $$
Answered by som(math1967) last updated on 10/Dec/22
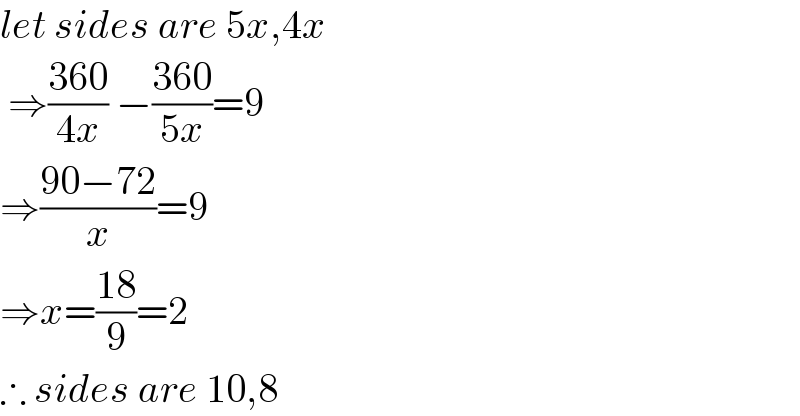
$${let}\:{sides}\:{are}\:\mathrm{5}{x},\mathrm{4}{x} \\ $$$$\:\Rightarrow\frac{\mathrm{360}}{\mathrm{4}{x}}\:−\frac{\mathrm{360}}{\mathrm{5}{x}}=\mathrm{9} \\ $$$$\Rightarrow\frac{\mathrm{90}−\mathrm{72}}{{x}}=\mathrm{9} \\ $$$$\Rightarrow{x}=\frac{\mathrm{18}}{\mathrm{9}}=\mathrm{2} \\ $$$$\therefore\:{sides}\:{are}\:\mathrm{10},\mathrm{8} \\ $$
Commented by Acem last updated on 10/Dec/22

$${Thanksss}\:{Sir}! \\ $$
Commented by som(math1967) last updated on 10/Dec/22
����
Commented by Acem last updated on 10/Dec/22

$${Coeur}\:\:\left(:\right. \\ $$
Answered by Acem last updated on 10/Dec/22
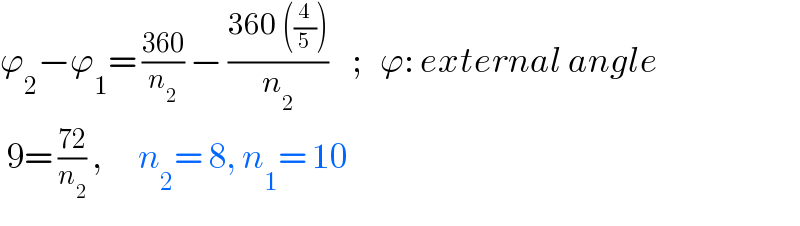
$$\varphi_{\mathrm{2}} −\varphi_{\mathrm{1}} =\:\frac{\mathrm{360}}{{n}_{\mathrm{2}} }\:−\:\frac{\mathrm{360}\:\left(\frac{\mathrm{4}}{\mathrm{5}}\right)}{{n}_{\mathrm{2}} }\:\:\:\:;\:\:\:\varphi:\:{external}\:{angle} \\ $$$$\:\mathrm{9}=\:\frac{\mathrm{72}}{{n}_{\mathrm{2}} }\:,\:\:\:\:\:\:{n}_{\mathrm{2}} =\:\mathrm{8},\:{n}_{\mathrm{1}} =\:\mathrm{10} \\ $$$$\: \\ $$
