
Question Number 212999 by golsendro last updated on 28/Oct/24
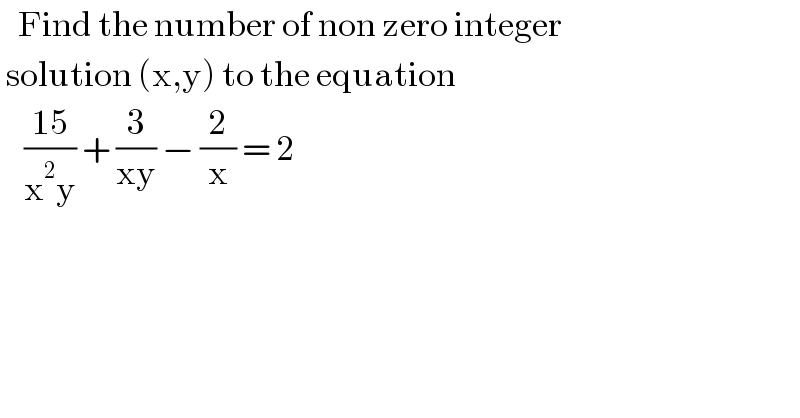
$$\:\:\:\mathrm{Find}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{non}\:\mathrm{zero}\:\mathrm{integer}\: \\ $$$$\:\mathrm{solution}\:\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{to}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$$\:\:\:\:\frac{\mathrm{15}}{\mathrm{x}^{\mathrm{2}} \mathrm{y}}\:+\:\frac{\mathrm{3}}{\mathrm{xy}}\:−\:\frac{\mathrm{2}}{\mathrm{x}}\:=\:\mathrm{2}\: \\ $$
Answered by A5T last updated on 28/Oct/24
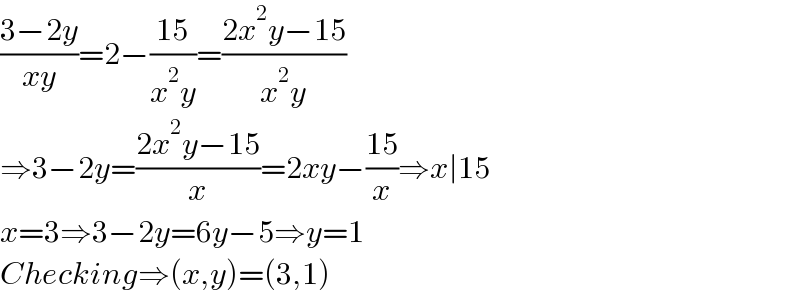
$$\frac{\mathrm{3}−\mathrm{2}{y}}{{xy}}=\mathrm{2}−\frac{\mathrm{15}}{{x}^{\mathrm{2}} {y}}=\frac{\mathrm{2}{x}^{\mathrm{2}} {y}−\mathrm{15}}{{x}^{\mathrm{2}} {y}} \\ $$$$\Rightarrow\mathrm{3}−\mathrm{2}{y}=\frac{\mathrm{2}{x}^{\mathrm{2}} {y}−\mathrm{15}}{{x}}=\mathrm{2}{xy}−\frac{\mathrm{15}}{{x}}\Rightarrow{x}\mid\mathrm{15} \\ $$$${x}=\mathrm{3}\Rightarrow\mathrm{3}−\mathrm{2}{y}=\mathrm{6}{y}−\mathrm{5}\Rightarrow{y}=\mathrm{1} \\ $$$${Checking}\Rightarrow\left({x},{y}\right)=\left(\mathrm{3},\mathrm{1}\right) \\ $$
