
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 49408 by rahul 19 last updated on 06/Dec/18

$${Find}\:{the}\:{number}\:{of}\:{all}\:{such}\:\mathrm{7}−{digit} \\ $$$${no}.\:{which}\:{satisfy}\:{conditions}: \\ $$$$\left.\mathrm{1}\right)\:{divisible}\:{by}\:\mathrm{3} \\ $$$$\left.\mathrm{2}\right)\:{repetition}\:{allowed} \\ $$$$\left.\mathrm{3}\right)\:{zero}\:{is}\:{not}\:{used}. \\ $$
Commented by mr W last updated on 06/Dec/18

$${there}\:{are}\:{only}\:{three}\:{kinds}\:{of}\:{numbers}: \\ $$$$\mathrm{3}{n}+{k}\:{with}\:{k}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$${we}\:{need}\:{only}\:{the}\:{numbers}\:{with}\:{k}=\mathrm{0}. \\ $$$${i}.{e}.\:{only}\:{a}\:{third}\:{of}\:\mathrm{9}^{\mathrm{7}} \:{numbers}\:{can}\:{be} \\ $$$${divided}\:{by}\:\mathrm{3},\:{so}\:{the}\:{answer}\:{is} \\ $$$$\frac{\mathrm{9}^{\mathrm{7}} }{\mathrm{3}}=\frac{\mathrm{4782969}}{\mathrm{3}}=\mathrm{1594323} \\ $$
Commented by Kunal12588 last updated on 06/Dec/18

$${there}\:{are}\:\mathrm{9}^{\mathrm{7}} =\mathrm{4782969}\:{which}\:{satisfies}\:\mathrm{2}^{{nd}} \: \\ $$$${and}\:\mathrm{3}^{{rd}} \:{condition}\:{the}\:{problem}\:{is}\:\mathrm{1}^{{st}} \:{condition} \\ $$
Commented by rahul 19 last updated on 06/Dec/18
Yes, the problem is tough. As all three conditions must be satisfied simultaneously!
Answered by MJS last updated on 06/Dec/18

$$\mathrm{all}\:\mathrm{6}−\mathrm{digit}\:\mathrm{numbers}\:\mathrm{without}\:\mathrm{zero} \\ $$$$\mathrm{9}^{\mathrm{6}} =\mathrm{531441} \\ $$$$\mathrm{each}\:\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{of}\:\mathrm{them}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{3}\:\mathrm{with}\:\mathrm{remainers}\:\mathrm{0},\:\mathrm{1},\:\mathrm{2} \\ $$$$\mathrm{add}\:\mathrm{3},\:\mathrm{2},\:\mathrm{1}\:\mathrm{as}\:\mathrm{7}^{\mathrm{th}} \:\mathrm{digit}\:\mathrm{and}\:\mathrm{they}'\mathrm{re}\:\mathrm{all}\:\mathrm{divisible} \\ $$$$\mathrm{by}\:\mathrm{3}\:\mathrm{with}\:\mathrm{remainder}\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{531441}\:\mathrm{numbers}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{conditions} \\ $$
Commented by MJS last updated on 06/Dec/18

$$\mathrm{1111113}\:\:\:\:\:\mathrm{1111212}\:\:\:\:\:... \\ $$$$\mathrm{1111122}\:\:\:\:\:\mathrm{1111221} \\ $$$$\mathrm{1111131}\:\:\:\:\:\mathrm{1111233} \\ $$$$\mathrm{1111143}\:\:\:\:\:\mathrm{1111242} \\ $$$$\mathrm{1111152}\:\:\:\:\:\mathrm{1111251} \\ $$$$\mathrm{1111161}\:\:\:\:\:\mathrm{1111263} \\ $$$$\mathrm{1111173}\:\:\:\:\:\mathrm{1111272} \\ $$$$\mathrm{1111182}\:\:\:\:\:\mathrm{1111281} \\ $$$$\mathrm{1111191}\:\:\:\:\:\mathrm{1111293} \\ $$
Commented by mr W last updated on 06/Dec/18
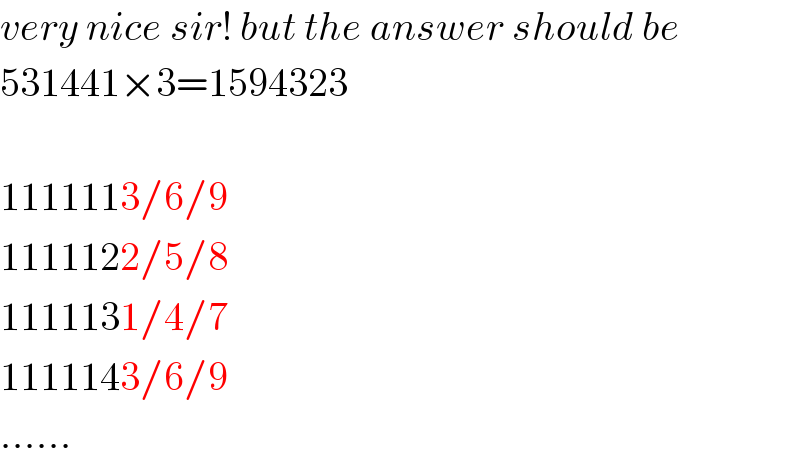
$${very}\:{nice}\:{sir}!\:{but}\:{the}\:{answer}\:{should}\:{be} \\ $$$$\mathrm{531441}×\mathrm{3}=\mathrm{1594323} \\ $$$$ \\ $$$$\mathrm{1111113}/\mathrm{6}/\mathrm{9} \\ $$$$\mathrm{1111122}/\mathrm{5}/\mathrm{8} \\ $$$$\mathrm{1111131}/\mathrm{4}/\mathrm{7} \\ $$$$\mathrm{1111143}/\mathrm{6}/\mathrm{9} \\ $$$$...... \\ $$
Commented by MJS last updated on 06/Dec/18

$$\mathrm{you}'\mathrm{re}\:\mathrm{absolutely}\:\mathrm{right}!\:\mathrm{I}\:\mathrm{had}\:\mathrm{been}\:\mathrm{in}\:\mathrm{a}\:\mathrm{hurry} \\ $$$$\mathrm{but}\:\mathrm{anyway}\:\mathrm{thought}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{these} \\ $$$$\mathrm{numbers}\:\mathrm{is}\:\mathrm{too}\:\mathrm{small}... \\ $$
