
Question Number 12226 by tawa last updated on 16/Apr/17

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{nth}\:\mathrm{term}\:\mathrm{of}\:\mathrm{this}\:\mathrm{sequence} \\ $$$$\mathrm{3},\:\mathrm{18},\:\mathrm{45},\:\mathrm{84},\:\mathrm{135}\:... \\ $$
Answered by ajfour last updated on 16/Apr/17

$${T}_{{n}} \:=\:\mathrm{3}\boldsymbol{{n}}\left(\mathrm{2}\boldsymbol{{n}}−\mathrm{1}\right)\:. \\ $$
Commented by tawa last updated on 16/Apr/17

$$\mathrm{Workings}\:\mathrm{plesse}\:!...\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by mrW1 last updated on 16/Apr/17

$$\mathrm{3}=\mathrm{3}×\mathrm{1}×\mathrm{1} \\ $$$$\mathrm{18}=\mathrm{3}×\mathrm{6}=\mathrm{3}×\mathrm{2}×\mathrm{3} \\ $$$$\mathrm{45}=\mathrm{3}×\mathrm{15}=\mathrm{3}×\mathrm{3}×\mathrm{5} \\ $$$$\mathrm{84}=\mathrm{3}×\mathrm{28}=\mathrm{3}×\mathrm{4}×\mathrm{7} \\ $$$$\mathrm{135}=\mathrm{3}×\mathrm{45}=\mathrm{3}×\mathrm{5}×\mathrm{9} \\ $$$$\Rightarrow\mathrm{3}×{n}×\left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$
Commented by ajfour last updated on 16/Apr/17
![1×3 , 2×9 , 3×15 , 4×21 , 5×27, .. 3[ 1×1 , 2×3 , 3×5 , 4×7 , 5×9 , ..] so 3n(2n−1) .](Q12231.png)
$$\mathrm{1}×\mathrm{3}\:,\:\mathrm{2}×\mathrm{9}\:,\:\mathrm{3}×\mathrm{15}\:,\:\mathrm{4}×\mathrm{21}\:,\:\mathrm{5}×\mathrm{27},\:.. \\ $$$$\mathrm{3}\left[\:\mathrm{1}×\mathrm{1}\:,\:\mathrm{2}×\mathrm{3}\:,\:\mathrm{3}×\mathrm{5}\:,\:\mathrm{4}×\mathrm{7}\:,\:\mathrm{5}×\mathrm{9}\:,\:..\right] \\ $$$${so}\:\:\mathrm{3}{n}\left(\mathrm{2}{n}−\mathrm{1}\right)\:. \\ $$
Commented by tawa last updated on 16/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by sandy_suhendra last updated on 16/Apr/17
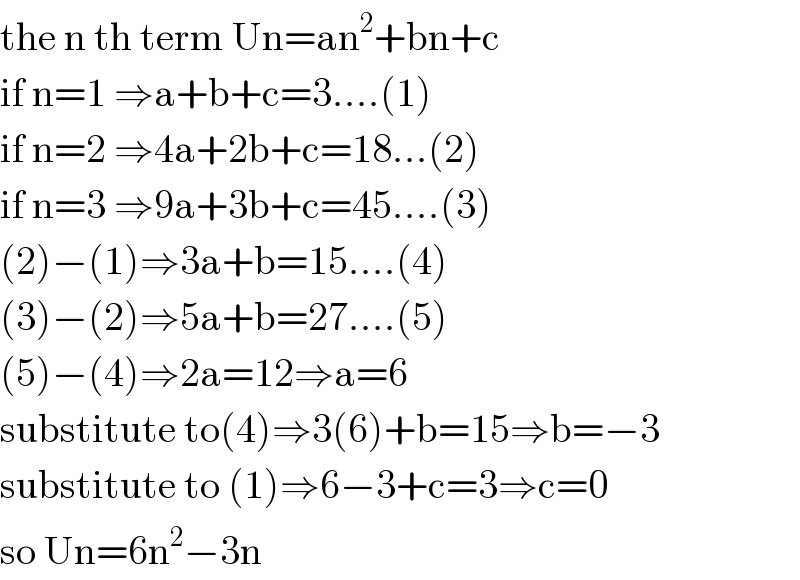
$$\mathrm{the}\:\mathrm{n}\:\mathrm{th}\:\mathrm{term}\:\mathrm{Un}=\mathrm{an}^{\mathrm{2}} +\mathrm{bn}+\mathrm{c} \\ $$$$\mathrm{if}\:\mathrm{n}=\mathrm{1}\:\Rightarrow\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{3}....\left(\mathrm{1}\right) \\ $$$$\mathrm{if}\:\mathrm{n}=\mathrm{2}\:\Rightarrow\mathrm{4a}+\mathrm{2b}+\mathrm{c}=\mathrm{18}...\left(\mathrm{2}\right) \\ $$$$\mathrm{if}\:\mathrm{n}=\mathrm{3}\:\Rightarrow\mathrm{9a}+\mathrm{3b}+\mathrm{c}=\mathrm{45}....\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{1}\right)\Rightarrow\mathrm{3a}+\mathrm{b}=\mathrm{15}....\left(\mathrm{4}\right) \\ $$$$\left(\mathrm{3}\right)−\left(\mathrm{2}\right)\Rightarrow\mathrm{5a}+\mathrm{b}=\mathrm{27}....\left(\mathrm{5}\right) \\ $$$$\left(\mathrm{5}\right)−\left(\mathrm{4}\right)\Rightarrow\mathrm{2a}=\mathrm{12}\Rightarrow\mathrm{a}=\mathrm{6} \\ $$$$\mathrm{substitute}\:\mathrm{to}\left(\mathrm{4}\right)\Rightarrow\mathrm{3}\left(\mathrm{6}\right)+\mathrm{b}=\mathrm{15}\Rightarrow\mathrm{b}=−\mathrm{3}\:\:\:\:\: \\ $$$$\mathrm{substitute}\:\mathrm{to}\:\left(\mathrm{1}\right)\Rightarrow\mathrm{6}−\mathrm{3}+\mathrm{c}=\mathrm{3}\Rightarrow\mathrm{c}=\mathrm{0}\:\:\:\:\: \\ $$$$\mathrm{so}\:\mathrm{Un}=\mathrm{6n}^{\mathrm{2}} −\mathrm{3n} \\ $$
Commented by sandy_suhendra last updated on 16/Apr/17
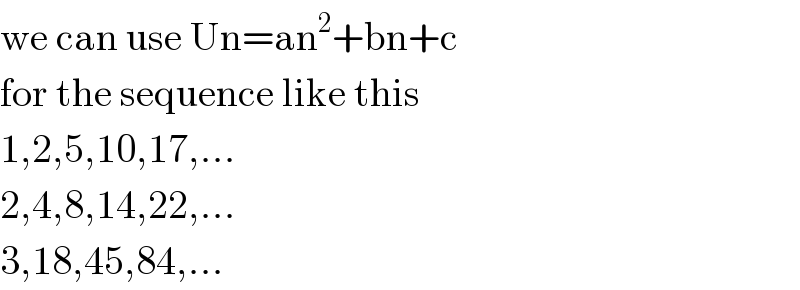
$$\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:\mathrm{Un}=\mathrm{an}^{\mathrm{2}} +\mathrm{bn}+\mathrm{c} \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{sequence}\:\mathrm{like}\:\mathrm{this} \\ $$$$\mathrm{1},\mathrm{2},\mathrm{5},\mathrm{10},\mathrm{17},... \\ $$$$\mathrm{2},\mathrm{4},\mathrm{8},\mathrm{14},\mathrm{22},... \\ $$$$\mathrm{3},\mathrm{18},\mathrm{45},\mathrm{84},... \\ $$
Commented by tawa last updated on 16/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
