Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 206532 by necx122 last updated on 17/Apr/24

Find the nth term of the sequence 0,3,8,15,24,......

$${Find}\:{the}\:{nth}\:{term}\:{of}\:{the}\:{sequence} \\ $$$$\mathrm{0},\mathrm{3},\mathrm{8},\mathrm{15},\mathrm{24},...... \\ $$

Answered by Berbere last updated on 17/Apr/24

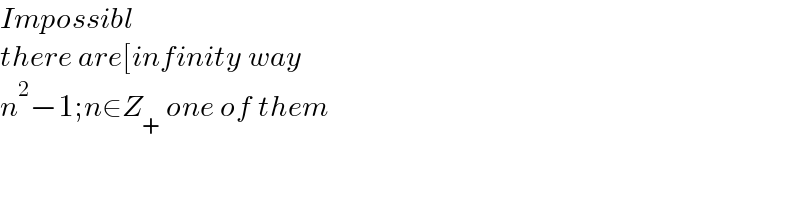
Impossibl there are[infinity way n^2 −1;n∈Z_+ one of them

$${Impossibl} \\ $$$${there}\:{are}\left[{infinity}\:{way}\:\right. \\ $$$${n}^{\mathrm{2}} −\mathrm{1};{n}\in{Z}_{+} \:{one}\:{of}\:{them} \\ $$

Answered by BaliramKumar last updated on 18/Apr/24

0 _(+3) 3 _(+5) 8 _(+7) 15 _(+9) 24 ......... a = 3 d = 5 − 3 = 2 S_(n−1) = ((n − 1)/2)[2×3 +(n −1−1)×2] S_(n−1) = (n−1)[3 +(n −1−1)] S_(n−1) = (n−1)(n +1) = n^2 − 1 U_1 + S_(n−1) = U_n = 0 + n^2 − 1 U_n = n^2 − 1

$$\mathrm{0}\underset{+\mathrm{3}} {\underbrace{\:\:\:\:\:\:}}\mathrm{3}\underset{+\mathrm{5}} {\underbrace{\:\:\:\:\:\:\:\:}}\mathrm{8}\underset{+\mathrm{7}} {\underbrace{\:\:\:\:\:\:\:\:}}\mathrm{15}\underset{+\mathrm{9}} {\underbrace{\:\:\:\:\:\:\:\:\:\:}}\mathrm{24}\:\:\:\:\:......... \\ $$$$\:\:\:{a}\:=\:\mathrm{3}\:\:\:\:\:\:\:\:\:{d}\:=\:\mathrm{5}\:−\:\mathrm{3}\:=\:\mathrm{2} \\ $$$$\mathrm{S}_{\mathrm{n}−\mathrm{1}} \:=\:\frac{\mathrm{n}\:−\:\mathrm{1}}{\mathrm{2}}\left[\mathrm{2}×\mathrm{3}\:+\left(\mathrm{n}\:−\mathrm{1}−\mathrm{1}\right)×\mathrm{2}\right] \\ $$$$\mathrm{S}_{\mathrm{n}−\mathrm{1}} \:=\:\left(\mathrm{n}−\mathrm{1}\right)\left[\mathrm{3}\:+\left(\mathrm{n}\:−\mathrm{1}−\mathrm{1}\right)\right] \\ $$$$\mathrm{S}_{\mathrm{n}−\mathrm{1}} \:=\:\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}\:+\mathrm{1}\right)\:=\:\mathrm{n}^{\mathrm{2}} \:−\:\mathrm{1} \\ $$$$\mathrm{U}_{\mathrm{1}} \:+\:\mathrm{S}_{\mathrm{n}−\mathrm{1}} \:=\:\mathrm{U}_{\mathrm{n}} \:=\:\:\mathrm{0}\:+\:\mathrm{n}^{\mathrm{2}} −\:\mathrm{1} \\ $$$$\:\mathrm{U}_{\mathrm{n}} \:=\:\mathrm{n}^{\mathrm{2}} −\:\mathrm{1} \\ $$

Commented by necx122 last updated on 18/Apr/24

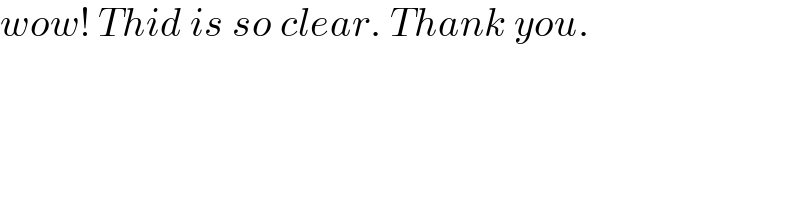
wow! Thid is so clear. Thank you.

$${wow}!\:{Thid}\:{is}\:{so}\:{clear}.\:{Thank}\:{you}. \\ $$

Answered by Frix last updated on 17/Apr/24

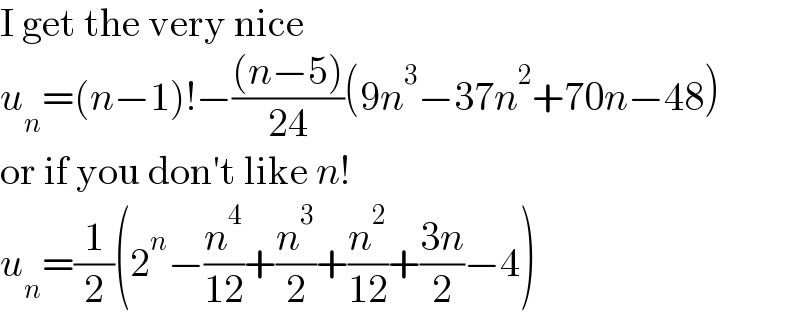
I get the very nice u_n =(n−1)!−(((n−5))/(24))(9n^3 −37n^2 +70n−48) or if you don′t like n! u_n =(1/2)(2^n −(n^4 /(12))+(n^3 /2)+(n^2 /(12))+((3n)/2)−4)

$$\mathrm{I}\:\mathrm{get}\:\mathrm{the}\:\mathrm{very}\:\mathrm{nice} \\ $$$${u}_{{n}} =\left({n}−\mathrm{1}\right)!−\frac{\left({n}−\mathrm{5}\right)}{\mathrm{24}}\left(\mathrm{9}{n}^{\mathrm{3}} −\mathrm{37}{n}^{\mathrm{2}} +\mathrm{70}{n}−\mathrm{48}\right) \\ $$$$\mathrm{or}\:\mathrm{if}\:\mathrm{you}\:\mathrm{don}'\mathrm{t}\:\mathrm{like}\:{n}! \\ $$$${u}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}^{{n}} −\frac{{n}^{\mathrm{4}} }{\mathrm{12}}+\frac{{n}^{\mathrm{3}} }{\mathrm{2}}+\frac{{n}^{\mathrm{2}} }{\mathrm{12}}+\frac{\mathrm{3}{n}}{\mathrm{2}}−\mathrm{4}\right) \\ $$

Commented by BaliramKumar last updated on 18/Apr/24

how to find?

$$\mathrm{how}\:\mathrm{to}\:\mathrm{find}? \\ $$

Commented by Frix last updated on 18/Apr/24

Just be creative.

$$\mathrm{Just}\:\mathrm{be}\:\mathrm{creative}. \\ $$

Commented by BaliramKumar last updated on 19/Apr/24

not true for n ≥ 6

$$\mathrm{not}\:\mathrm{true}\:\mathrm{for}\:\:\:\:\mathrm{n}\:\geq\:\mathrm{6} \\ $$

Commented by mr W last updated on 19/Apr/24

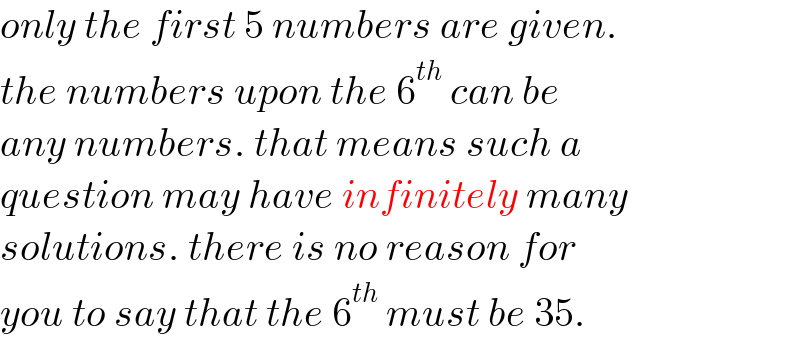
only the first 5 numbers are given. the numbers upon the 6^(th) can be any numbers. that means such a question may have infinitely many solutions. there is no reason for you to say that the 6^(th) must be 35.

$${only}\:{the}\:{first}\:\mathrm{5}\:{numbers}\:{are}\:{given}. \\ $$$${the}\:{numbers}\:{upon}\:{the}\:\mathrm{6}^{{th}} \:{can}\:{be} \\ $$$${any}\:{numbers}.\:{that}\:{means}\:{such}\:{a} \\ $$$${question}\:{may}\:{have}\:{infinitely}\:{many} \\ $$$${solutions}.\:{there}\:{is}\:{no}\:{reason}\:{for} \\ $$$${you}\:{to}\:{say}\:{that}\:{the}\:\mathrm{6}^{{th}} \:{must}\:{be}\:\mathrm{35}. \\ $$

Commented by Frix last updated on 19/Apr/24

Usually we search for a polynome: n numbers given ⇒ polynome of degree n−1 In the following cases this gives the red next numbers: 0, 1, 2 0, 1, 1, 0 0, 1, 1, 2, 6 0, 1, 1, 2, 3, 0 0, 1, 1, 2, 3, 5, 16 0, 1, 1, 2, 3, 5, 8, 0 ... Think about it!

$$\mathrm{Usually}\:\mathrm{we}\:\mathrm{search}\:\mathrm{for}\:\mathrm{a}\:\mathrm{polynome}: \\ $$$${n}\:\mathrm{numbers}\:\mathrm{given}\:\Rightarrow\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{degree}\:{n}−\mathrm{1} \\ $$$$\mathrm{In}\:\mathrm{the}\:\mathrm{following}\:\mathrm{cases}\:\mathrm{this}\:\mathrm{gives}\:\mathrm{the}\:\mathrm{red}\: \\ $$$$\mathrm{next}\:\mathrm{numbers}: \\ $$$$\mathrm{0},\:\mathrm{1},\:\mathrm{2} \\ $$$$\mathrm{0},\:\mathrm{1},\:\mathrm{1},\:\mathrm{0} \\ $$$$\mathrm{0},\:\mathrm{1},\:\mathrm{1},\:\mathrm{2},\:\mathrm{6} \\ $$$$\mathrm{0},\:\mathrm{1},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{0} \\ $$$$\mathrm{0},\:\mathrm{1},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{5},\:\mathrm{16} \\ $$$$\mathrm{0},\:\mathrm{1},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{5},\:\mathrm{8},\:\mathrm{0} \\ $$$$... \\ $$$$\mathrm{Think}\:\mathrm{about}\:\mathrm{it}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com