Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 62664 by Cheyboy last updated on 24/Jun/19

Find the nth term 100,92,76,44,......

$${Find}\:{the}\:{nth}\:{term} \\ $$$$\mathrm{100},\mathrm{92},\mathrm{76},\mathrm{44},...... \\ $$

Answered by MJS last updated on 24/Jun/19

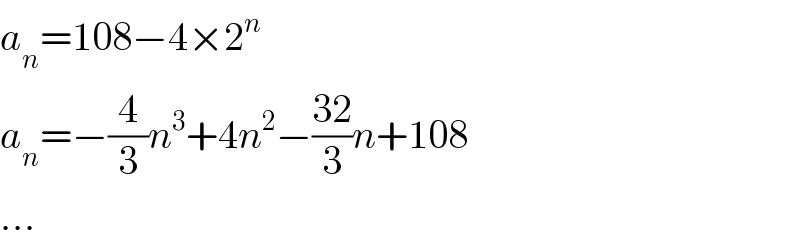
a_n =108−4×2^n a_n =−(4/3)n^3 +4n^2 −((32)/3)n+108 ...

$${a}_{{n}} =\mathrm{108}−\mathrm{4}×\mathrm{2}^{{n}} \\ $$$${a}_{{n}} =−\frac{\mathrm{4}}{\mathrm{3}}{n}^{\mathrm{3}} +\mathrm{4}{n}^{\mathrm{2}} −\frac{\mathrm{32}}{\mathrm{3}}{n}+\mathrm{108} \\ $$$$... \\ $$

Commented by ajfour last updated on 24/Jun/19

wonderful sir! how to expect and judge the first one?

Commented by mr W last updated on 24/Jun/19

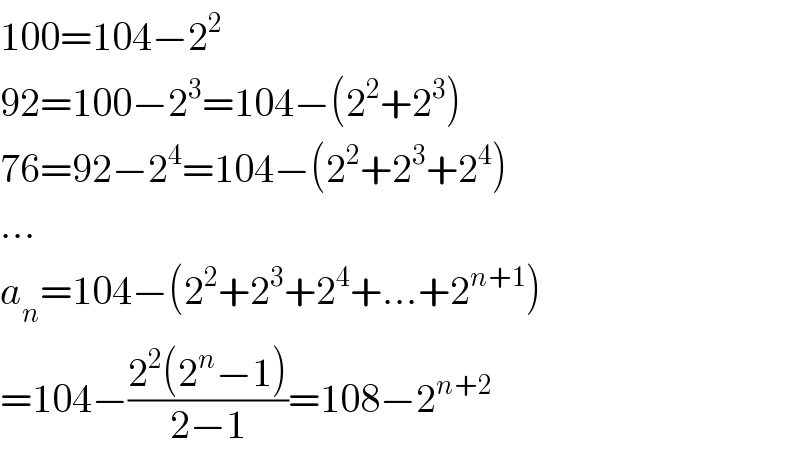
100=104−2^2 92=100−2^3 =104−(2^2 +2^3 ) 76=92−2^4 =104−(2^2 +2^3 +2^4 ) ... a_n =104−(2^2 +2^3 +2^4 +...+2^(n+1) ) =104−((2^2 (2^n −1))/(2−1))=108−2^(n+2)

$$\mathrm{100}=\mathrm{104}−\mathrm{2}^{\mathrm{2}} \\ $$$$\mathrm{92}=\mathrm{100}−\mathrm{2}^{\mathrm{3}} =\mathrm{104}−\left(\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} \right) \\ $$$$\mathrm{76}=\mathrm{92}−\mathrm{2}^{\mathrm{4}} =\mathrm{104}−\left(\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{4}} \right) \\ $$$$... \\ $$$${a}_{{n}} =\mathrm{104}−\left(\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{4}} +...+\mathrm{2}^{{n}+\mathrm{1}} \right) \\ $$$$=\mathrm{104}−\frac{\mathrm{2}^{\mathrm{2}} \left(\mathrm{2}^{{n}} −\mathrm{1}\right)}{\mathrm{2}−\mathrm{1}}=\mathrm{108}−\mathrm{2}^{{n}+\mathrm{2}} \\ $$

Commented by MJS last updated on 24/Jun/19

we can solve Σ_(i=1) ^4 c_i =100 Σ_(i=1) ^4 c_i ^2 =92 Σ_(i=1) ^4 c_i ^3 =76 Σ_(i=1) ^4 c_i ^4 =44 using c_(1, 2) =α±(√β); c_(3, 4) =γ±(√δ) ⇒ a_n =Σ_(i=1) ^4 c_i ^n but the solution doesn′t look very nice

$$\mathrm{we}\:\mathrm{can}\:\mathrm{solve} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{c}_{{i}} =\mathrm{100} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{c}_{{i}} ^{\mathrm{2}} =\mathrm{92} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{c}_{{i}} ^{\mathrm{3}} =\mathrm{76} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{c}_{{i}} ^{\mathrm{4}} =\mathrm{44} \\ $$$$\mathrm{using}\:{c}_{\mathrm{1},\:\mathrm{2}} =\alpha\pm\sqrt{\beta};\:{c}_{\mathrm{3},\:\mathrm{4}} =\gamma\pm\sqrt{\delta} \\ $$$$\Rightarrow\:{a}_{{n}} =\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{c}_{{i}} ^{{n}} \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{look}\:\mathrm{very}\:\mathrm{nice} \\ $$

Commented by Cheyboy last updated on 25/Jun/19

Thank you very much

$${Thank}\:{you}\:{very}\:{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com