Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 116348 by Dwaipayan Shikari last updated on 03/Oct/20

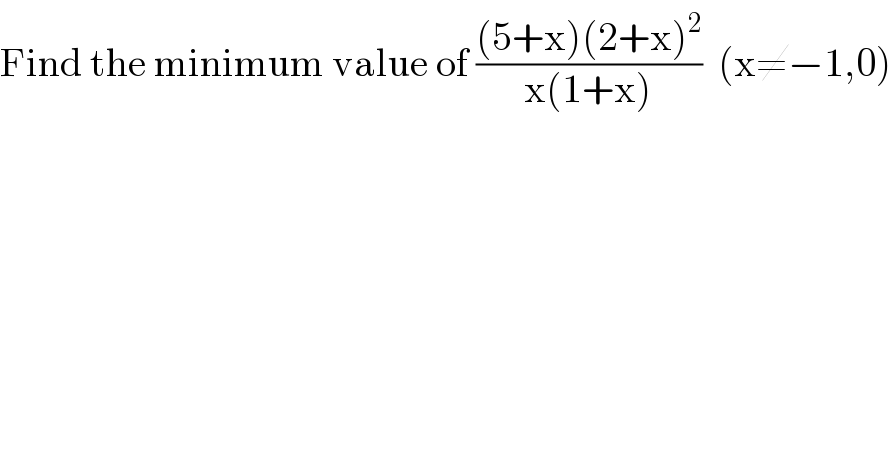
Find the minimum value of (((5+x)(2+x)^2 )/(x(1+x))) (x≠−1,0)

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:\frac{\left(\mathrm{5}+\mathrm{x}\right)\left(\mathrm{2}+\mathrm{x}\right)^{\mathrm{2}} }{\mathrm{x}\left(\mathrm{1}+\mathrm{x}\right)}\:\:\left(\mathrm{x}\neq−\mathrm{1},\mathrm{0}\right) \\ $$

Commented by MJS_new last updated on 03/Oct/20

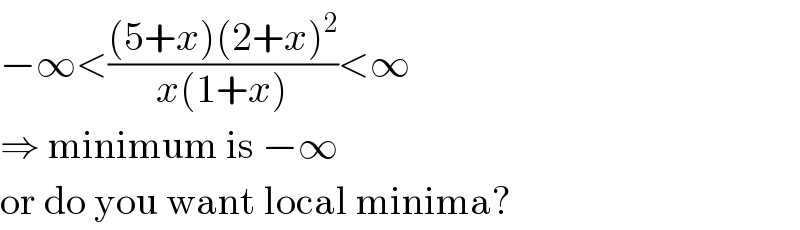
−∞<(((5+x)(2+x)^2 )/(x(1+x)))<∞ ⇒ minimum is −∞ or do you want local minima?

$$−\infty<\frac{\left(\mathrm{5}+{x}\right)\left(\mathrm{2}+{x}\right)^{\mathrm{2}} }{{x}\left(\mathrm{1}+{x}\right)}<\infty \\ $$$$\Rightarrow\:\mathrm{minimum}\:\mathrm{is}\:−\infty \\ $$$$\mathrm{or}\:\mathrm{do}\:\mathrm{you}\:\mathrm{want}\:\mathrm{local}\:\mathrm{minima}? \\ $$

Commented by Dwaipayan Shikari last updated on 03/Oct/20

Yes

$$\mathrm{Yes} \\ $$

Answered by MJS_new last updated on 03/Oct/20

y=(((x+2)^2 (x+5))/(x(x+1))) y′=(((x+2)(x^3 −15x−10))/(x^2 (x+1)^2 )) y′′=((8(4x^3 +15x^2 +15x+5))/(x^3 (x+1)^3 )) y′=0 ⇒ x_1 ≈−3.48261∧y≈.385778; y′′<0 ⇒ local max x_2 =−2∧y=0; y′′>0 ⇒ local min x_3 ≈−.688417∧y≈−34.5782; y′′<0 ⇒ local max x_4 ≈4.17103∧y≈16.1925; y′′>0 ⇒ local min

$${y}=\frac{\left({x}+\mathrm{2}\right)^{\mathrm{2}} \left({x}+\mathrm{5}\right)}{{x}\left({x}+\mathrm{1}\right)} \\ $$$${y}'=\frac{\left({x}+\mathrm{2}\right)\left({x}^{\mathrm{3}} −\mathrm{15}{x}−\mathrm{10}\right)}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${y}''=\frac{\mathrm{8}\left(\mathrm{4}{x}^{\mathrm{3}} +\mathrm{15}{x}^{\mathrm{2}} +\mathrm{15}{x}+\mathrm{5}\right)}{{x}^{\mathrm{3}} \left({x}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${y}'=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1}} \approx−\mathrm{3}.\mathrm{48261}\wedge{y}\approx.\mathrm{385778};\:{y}''<\mathrm{0}\:\Rightarrow\:\mathrm{local}\:\mathrm{max} \\ $$$${x}_{\mathrm{2}} =−\mathrm{2}\wedge{y}=\mathrm{0};\:{y}''>\mathrm{0}\:\Rightarrow\:\mathrm{local}\:\mathrm{min} \\ $$$${x}_{\mathrm{3}} \approx−.\mathrm{688417}\wedge{y}\approx−\mathrm{34}.\mathrm{5782};\:{y}''<\mathrm{0}\:\Rightarrow\:\mathrm{local}\:\mathrm{max} \\ $$$${x}_{\mathrm{4}} \approx\mathrm{4}.\mathrm{17103}\wedge{y}\approx\mathrm{16}.\mathrm{1925};\:{y}''>\mathrm{0}\:\Rightarrow\:\mathrm{local}\:\mathrm{min} \\ $$

Commented by Dwaipayan Shikari last updated on 03/Oct/20

Thanking you

$$\mathrm{Thanking}\:\mathrm{you} \\ $$

Commented by MJS_new last updated on 03/Oct/20

you′re welcome the exact values of the roots if the 3^(rd) degree polynomial are not useful in this case

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$$$\mathrm{the}\:\mathrm{exact}\:\mathrm{values}\:\mathrm{of}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{if}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree} \\ $$$$\mathrm{polynomial}\:\mathrm{are}\:\mathrm{not}\:\mathrm{useful}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com