Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 191862 by cortano12 last updated on 02/May/23

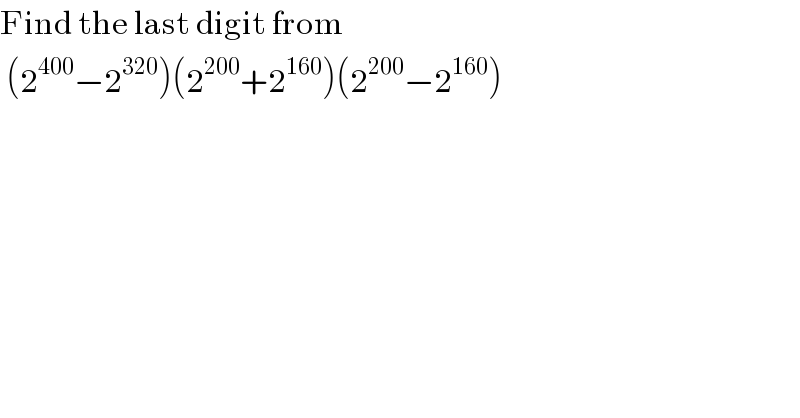
Find the last digit from (2^(400) −2^(320) )(2^(200) +2^(160) )(2^(200) −2^(160) )

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{last}\:\mathrm{digit}\:\mathrm{from}\: \\ $$$$\:\left(\mathrm{2}^{\mathrm{400}} −\mathrm{2}^{\mathrm{320}} \right)\left(\mathrm{2}^{\mathrm{200}} +\mathrm{2}^{\mathrm{160}} \right)\left(\mathrm{2}^{\mathrm{200}} −\mathrm{2}^{\mathrm{160}} \right) \\ $$

Commented by BaliramKumar last updated on 02/May/23

0

$$\mathrm{0} \\ $$

Answered by Subhi last updated on 02/May/23

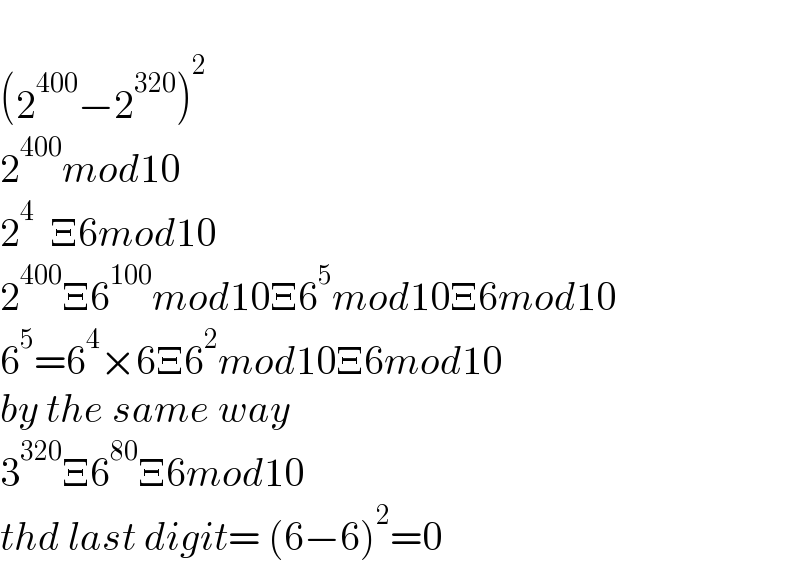
(2^(400) −2^(320) )^2 2^(400) mod10 2^4 Ξ6mod10 2^(400) Ξ6^(100) mod10Ξ6^5 mod10Ξ6mod10 6^5 =6^4 ×6Ξ6^2 mod10Ξ6mod10 by the same way 3^(320) Ξ6^(80) Ξ6mod10 thd last digit= (6−6)^2 =0

$$ \\ $$$$\left(\mathrm{2}^{\mathrm{400}} −\mathrm{2}^{\mathrm{320}} \right)^{\mathrm{2}} \\ $$$$\mathrm{2}^{\mathrm{400}} {mod}\mathrm{10}\: \\ $$$$\mathrm{2}^{\mathrm{4}} \:\:\Xi\mathrm{6}{mod}\mathrm{10} \\ $$$$\mathrm{2}^{\mathrm{400}} \Xi\mathrm{6}^{\mathrm{100}} {mod}\mathrm{10}\Xi\mathrm{6}^{\mathrm{5}} {mod}\mathrm{10}\Xi\mathrm{6}{mod}\mathrm{10} \\ $$$$\mathrm{6}^{\mathrm{5}} =\mathrm{6}^{\mathrm{4}} ×\mathrm{6}\Xi\mathrm{6}^{\mathrm{2}} {mod}\mathrm{10}\Xi\mathrm{6}{mod}\mathrm{10} \\ $$$${by}\:{the}\:{same}\:{way}\: \\ $$$$\mathrm{3}^{\mathrm{320}} \Xi\mathrm{6}^{\mathrm{80}} \Xi\mathrm{6}{mod}\mathrm{10} \\ $$$${thd}\:{last}\:{digit}=\:\left(\mathrm{6}−\mathrm{6}\right)^{\mathrm{2}} =\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com