Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 216077 by MATHEMATICSAM last updated on 27/Jan/25

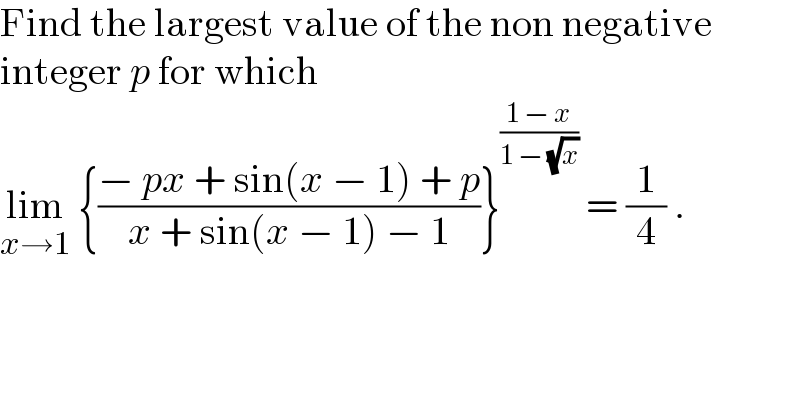
Find the largest value of the non negative integer p for which lim_(x→1) {((− px + sin(x − 1) + p)/(x + sin(x − 1) − 1))}^((1 − x)/(1 − (√x))) = (1/4) .

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{largest}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{non}\:\mathrm{negative} \\ $$$$\mathrm{integer}\:{p}\:\mathrm{for}\:\mathrm{which}\: \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left\{\frac{−\:{px}\:+\:\mathrm{sin}\left({x}\:−\:\mathrm{1}\right)\:+\:{p}}{{x}\:+\:\mathrm{sin}\left({x}\:−\:\mathrm{1}\right)\:−\:\mathrm{1}}\right\}^{\frac{\mathrm{1}\:−\:{x}}{\mathrm{1}\:−\:\sqrt{{x}}}} \:=\:\frac{\mathrm{1}}{\mathrm{4}}\:. \\ $$

Answered by mahdipoor last updated on 27/Jan/25

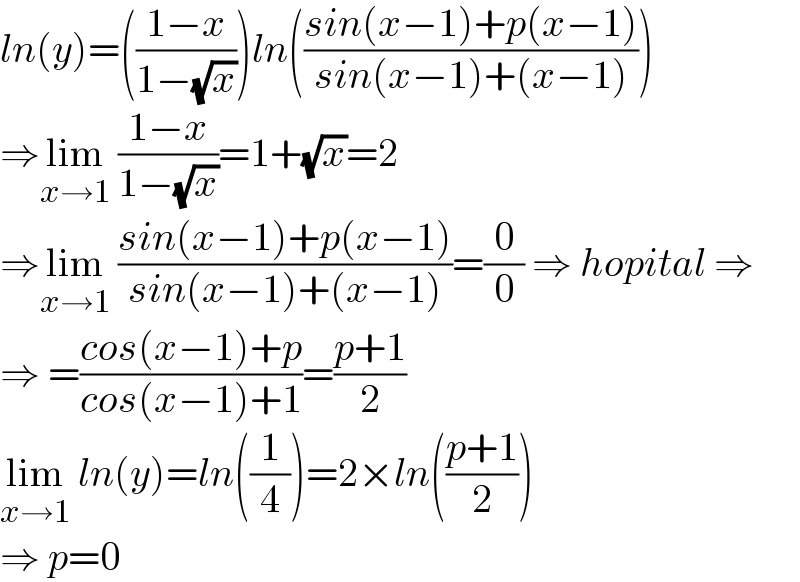
ln(y)=(((1−x)/(1−(√x))))ln(((sin(x−1)+p(x−1))/(sin(x−1)+(x−1)))) ⇒lim_(x→1) ((1−x)/(1−(√x)))=1+(√x)=2 ⇒lim_(x→1) ((sin(x−1)+p(x−1))/(sin(x−1)+(x−1)))=(0/0) ⇒ hopital ⇒ ⇒ =((cos(x−1)+p)/(cos(x−1)+1))=((p+1)/2) lim_(x→1) ln(y)=ln((1/4))=2×ln(((p+1)/2)) ⇒ p=0

$${ln}\left({y}\right)=\left(\frac{\mathrm{1}−{x}}{\mathrm{1}−\sqrt{{x}}}\right){ln}\left(\frac{{sin}\left({x}−\mathrm{1}\right)+{p}\left({x}−\mathrm{1}\right)}{{sin}\left({x}−\mathrm{1}\right)+\left({x}−\mathrm{1}\right)}\right) \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}−{x}}{\mathrm{1}−\sqrt{{x}}}=\mathrm{1}+\sqrt{{x}}=\mathrm{2} \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{sin}\left({x}−\mathrm{1}\right)+{p}\left({x}−\mathrm{1}\right)}{{sin}\left({x}−\mathrm{1}\right)+\left({x}−\mathrm{1}\right)}=\frac{\mathrm{0}}{\mathrm{0}}\:\Rightarrow\:{hopital}\:\Rightarrow \\ $$$$\Rightarrow\:=\frac{{cos}\left({x}−\mathrm{1}\right)+{p}}{{cos}\left({x}−\mathrm{1}\right)+\mathrm{1}}=\frac{{p}+\mathrm{1}}{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:{ln}\left({y}\right)={ln}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{2}×{ln}\left(\frac{{p}+\mathrm{1}}{\mathrm{2}}\right)\: \\ $$$$\Rightarrow\:{p}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com