
Question Number 165831 by HongKing last updated on 09/Feb/22
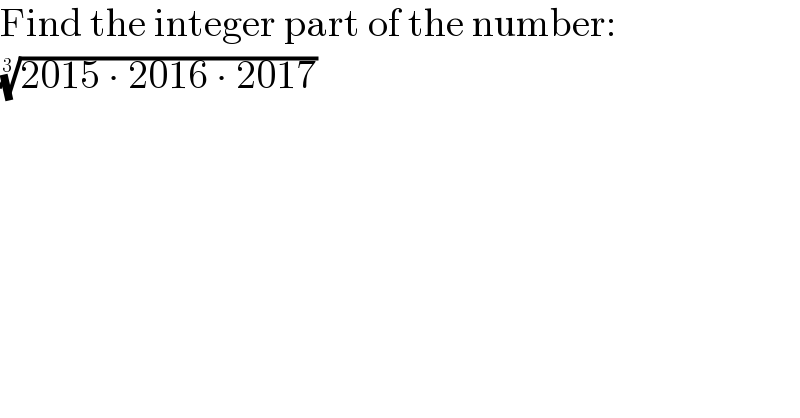
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{integer}\:\mathrm{part}\:\mathrm{of}\:\mathrm{the}\:\mathrm{number}: \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{2015}\:\centerdot\:\mathrm{2016}\:\centerdot\:\mathrm{2017}} \\ $$
Commented by mr W last updated on 09/Feb/22
![((x(x+1)(x+2)))^(1/3) >((x×x×x))^(1/3) =x ((x(x+1)(x+2)))^(1/3) =(((x+1)((x+1)^2 −1)))^(1/3) <(((x+1)(x+1)^2 ))^(1/3) =x+1 x<((x(x+1)(x+2)))^(1/3) <x+1 ⇒[((x(x+1)(x+2)))^(1/3) ]=x ⇒[((2015×2016×2017))^(1/3) =2015](Q165844.png)
$$\sqrt[{\mathrm{3}}]{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)} \\ $$$$>\sqrt[{\mathrm{3}}]{{x}×{x}×{x}}={x} \\ $$$$ \\ $$$$\sqrt[{\mathrm{3}}]{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}=\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)\left(\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$<\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)^{\mathrm{2}} }={x}+\mathrm{1} \\ $$$$ \\ $$$${x}<\sqrt[{\mathrm{3}}]{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}<{x}+\mathrm{1} \\ $$$$\Rightarrow\left[\sqrt[{\mathrm{3}}]{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}\right]={x} \\ $$$$ \\ $$$$\Rightarrow\left[\sqrt[{\mathrm{3}}]{\mathrm{2015}×\mathrm{2016}×\mathrm{2017}}=\mathrm{2015}\right. \\ $$
Answered by naka3546 last updated on 09/Feb/22
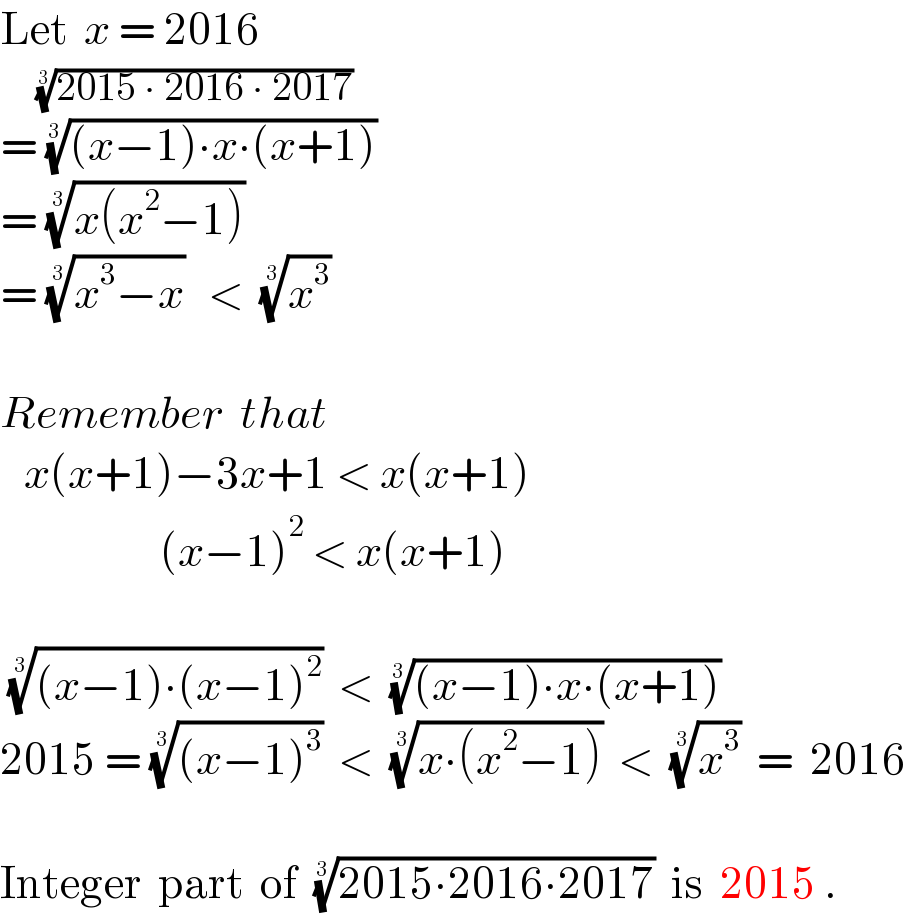
$$\mathrm{Let}\:\:{x}\:=\:\mathrm{2016} \\ $$$$\:\:\:\:\:\:\sqrt[{\mathrm{3}}]{\mathrm{2015}\:\centerdot\:\mathrm{2016}\:\centerdot\:\mathrm{2017}} \\ $$$$=\:\sqrt[{\mathrm{3}}]{\left({x}−\mathrm{1}\right)\centerdot{x}\centerdot\left({x}+\mathrm{1}\right)} \\ $$$$=\:\sqrt[{\mathrm{3}}]{{x}\left({x}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$=\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} −{x}}\:\:\:<\:\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} }\:\: \\ $$$$ \\ $$$${Remember}\:\:{that}\:\: \\ $$$$\:\:\:{x}\left({x}+\mathrm{1}\right)−\mathrm{3}{x}+\mathrm{1}\:<\:{x}\left({x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:<\:{x}\left({x}+\mathrm{1}\right) \\ $$$$ \\ $$$$\:\sqrt[{\mathrm{3}}]{\left({x}−\mathrm{1}\right)\centerdot\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:\:<\:\:\sqrt[{\mathrm{3}}]{\left({x}−\mathrm{1}\right)\centerdot{x}\centerdot\left({x}+\mathrm{1}\right)}\: \\ $$$$\mathrm{2015}\:=\:\sqrt[{\mathrm{3}}]{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }\:\:<\:\:\sqrt[{\mathrm{3}}]{{x}\centerdot\left({x}^{\mathrm{2}} −\mathrm{1}\right)}\:\:<\:\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} }\:\:=\:\:\mathrm{2016} \\ $$$$ \\ $$$$\mathrm{Integer}\:\:\mathrm{part}\:\:\mathrm{of}\:\:\sqrt[{\mathrm{3}}]{\mathrm{2015}\centerdot\mathrm{2016}\centerdot\mathrm{2017}}\:\:\mathrm{is}\:\:\mathrm{2015}\:. \\ $$
Commented by naka3546 last updated on 09/Feb/22

$${yes},\:{sir}. \\ $$
