Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 62945 by Tawa1 last updated on 27/Jun/19

Find the greatest coefficient in the expansion of (6 − 4x)^(−3)

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{coefficient}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of}\:\:\:\left(\mathrm{6}\:−\:\mathrm{4x}\right)^{−\mathrm{3}} \\ $$

Answered by mr W last updated on 27/Jun/19

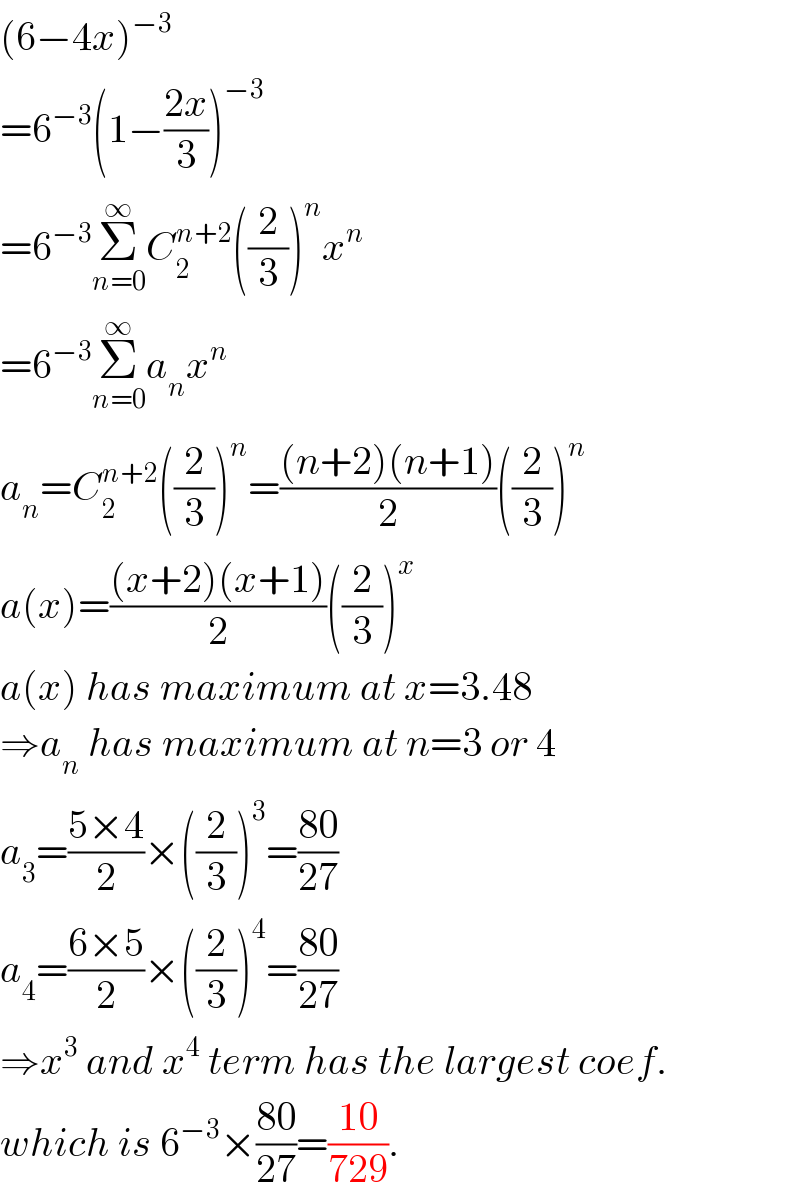
(6−4x)^(−3) =6^(−3) (1−((2x)/3))^(−3) =6^(−3) Σ_(n=0) ^∞ C_2 ^(n+2) ((2/3))^n x^n =6^(−3) Σ_(n=0) ^∞ a_n x^n a_n =C_2 ^(n+2) ((2/3))^n =(((n+2)(n+1))/2)((2/3))^n a(x)=(((x+2)(x+1))/2)((2/3))^x a(x) has maximum at x=3.48 ⇒a_n has maximum at n=3 or 4 a_3 =((5×4)/2)×((2/3))^3 =((80)/(27)) a_4 =((6×5)/2)×((2/3))^4 =((80)/(27)) ⇒x^3 and x^4 term has the largest coef. which is 6^(−3) ×((80)/(27))=((10)/(729)).

$$\left(\mathrm{6}−\mathrm{4}{x}\right)^{−\mathrm{3}} \\ $$$$=\mathrm{6}^{−\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{2}{x}}{\mathrm{3}}\right)^{−\mathrm{3}} \\ $$$$=\mathrm{6}^{−\mathrm{3}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{2}} ^{{n}+\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} {x}^{{n}} \\ $$$$=\mathrm{6}^{−\mathrm{3}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{a}_{{n}} {x}^{{n}} \\ $$$${a}_{{n}} ={C}_{\mathrm{2}} ^{{n}+\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} =\frac{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} \\ $$$${a}\left({x}\right)=\frac{\left({x}+\mathrm{2}\right)\left({x}+\mathrm{1}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} \\ $$$${a}\left({x}\right)\:{has}\:{maximum}\:{at}\:{x}=\mathrm{3}.\mathrm{48} \\ $$$$\Rightarrow{a}_{{n}} \:{has}\:{maximum}\:{at}\:{n}=\mathrm{3}\:{or}\:\mathrm{4} \\ $$$${a}_{\mathrm{3}} =\frac{\mathrm{5}×\mathrm{4}}{\mathrm{2}}×\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{3}} =\frac{\mathrm{80}}{\mathrm{27}} \\ $$$${a}_{\mathrm{4}} =\frac{\mathrm{6}×\mathrm{5}}{\mathrm{2}}×\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{4}} =\frac{\mathrm{80}}{\mathrm{27}} \\ $$$$\Rightarrow{x}^{\mathrm{3}} \:{and}\:{x}^{\mathrm{4}} \:{term}\:{has}\:{the}\:{largest}\:{coef}. \\ $$$${which}\:{is}\:\mathrm{6}^{−\mathrm{3}} ×\frac{\mathrm{80}}{\mathrm{27}}=\frac{\mathrm{10}}{\mathrm{729}}. \\ $$

Commented by Tawa1 last updated on 27/Jun/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 29/Jun/19

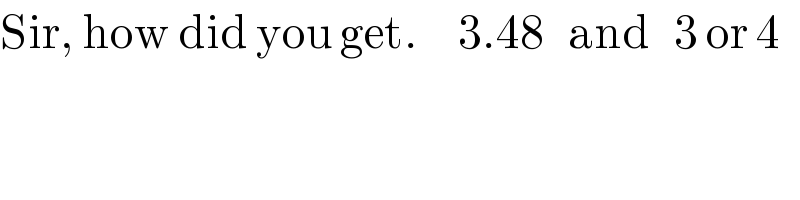
Sir, how did you get. 3.48 and 3 or 4

$$\mathrm{Sir},\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}.\:\:\:\:\:\mathrm{3}.\mathrm{48}\:\:\:\mathrm{and}\:\:\:\mathrm{3}\:\mathrm{or}\:\mathrm{4} \\ $$

Commented by mr W last updated on 29/Jun/19

look at a(x)=(((x+2)(x+1))/2)((2/3))^x (x+2)(x+1) is increasing with x, ((2/3))^x is decreasing with x, so an(x) has a maximum at some point, at this point ((da(x))/dx)=0. ((da(x))/dx)=(((2x+3))/2)((2/3))^x +(((x^2 +3x+1))/2)((2/3))^x ln ((2/3))=0 (2x+3)+(x^2 +3x+1)ln ((2/3))=0 ln ((2/3))x^2 +[3ln ((2/3))−2]x+[ln ((2/3))−3]=0 ⇒x=((−3ln ((2/3))+2+(√([3ln ((2/3))−2]^2 −4 ln ((2/3)) [ln ((2/3))−3])))/(2ln ((2/3))))=3.48 i.e. a(x) has maximum at x=3.48 a_n will have maximum when n is so close to 3.48 as possible, that is n=3 or n=4.

$${look}\:{at}\:{a}\left({x}\right)=\frac{\left({x}+\mathrm{2}\right)\left({x}+\mathrm{1}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} \\ $$$$\left({x}+\mathrm{2}\right)\left({x}+\mathrm{1}\right)\:{is}\:{increasing}\:{with}\:{x}, \\ $$$$\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} \:{is}\:{decreasing}\:{with}\:{x}, \\ $$$${so}\:{an}\left({x}\right)\:{has}\:{a}\:{maximum}\:{at}\:{some} \\ $$$${point},\:{at}\:{this}\:{point}\:\frac{{da}\left({x}\right)}{{dx}}=\mathrm{0}. \\ $$$$\frac{{da}\left({x}\right)}{{dx}}=\frac{\left(\mathrm{2}{x}+\mathrm{3}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} +\frac{\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} \mathrm{ln}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}{x}+\mathrm{3}\right)+\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)\mathrm{ln}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\mathrm{ln}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right){x}^{\mathrm{2}} +\left[\mathrm{3ln}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\mathrm{2}\right]{x}+\left[\mathrm{ln}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\mathrm{3}\right]=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{−\mathrm{3ln}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\mathrm{2}+\sqrt{\left[\mathrm{3ln}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\mathrm{2}\right]^{\mathrm{2}} −\mathrm{4}\:\mathrm{ln}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:\left[\mathrm{ln}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\mathrm{3}\right]}}{\mathrm{2ln}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)}=\mathrm{3}.\mathrm{48} \\ $$$${i}.{e}.\:{a}\left({x}\right)\:{has}\:{maximum}\:{at}\:{x}=\mathrm{3}.\mathrm{48} \\ $$$${a}_{{n}} \:{will}\:{have}\:{maximum}\:{when}\:{n}\:{is} \\ $$$${so}\:{close}\:{to}\:\mathrm{3}.\mathrm{48}\:{as}\:{possible},\:{that}\:{is} \\ $$$${n}=\mathrm{3}\:{or}\:{n}=\mathrm{4}. \\ $$

Commented by Tawa1 last updated on 29/Jun/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by mr W last updated on 13/Jul/19

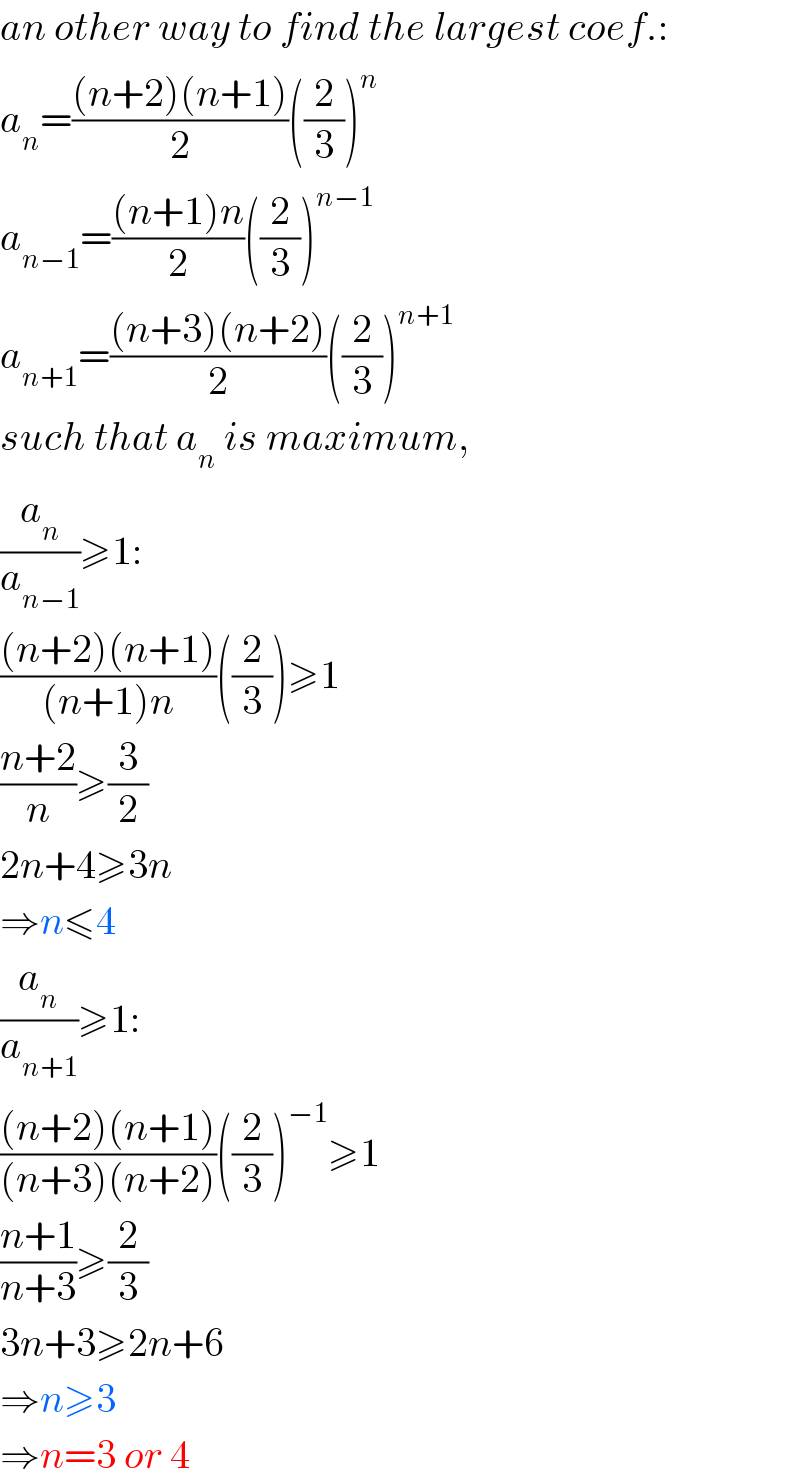
an other way to find the largest coef.: a_n =(((n+2)(n+1))/2)((2/3))^n a_(n−1) =(((n+1)n)/2)((2/3))^(n−1) a_(n+1) =(((n+3)(n+2))/2)((2/3))^(n+1) such that a_n is maximum, (a_n /a_(n−1) )≥1: (((n+2)(n+1))/((n+1)n))((2/3))≥1 ((n+2)/n)≥(3/2) 2n+4≥3n ⇒n≤4 (a_n /a_(n+1) )≥1: (((n+2)(n+1))/((n+3)(n+2)))((2/3))^(−1) ≥1 ((n+1)/(n+3))≥(2/3) 3n+3≥2n+6 ⇒n≥3 ⇒n=3 or 4

$${an}\:{other}\:{way}\:{to}\:{find}\:{the}\:{largest}\:{coef}.: \\ $$$${a}_{{n}} =\frac{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} \\ $$$${a}_{{n}−\mathrm{1}} =\frac{\left({n}+\mathrm{1}\right){n}}{\mathrm{2}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}−\mathrm{1}} \\ $$$${a}_{{n}+\mathrm{1}} =\frac{\left({n}+\mathrm{3}\right)\left({n}+\mathrm{2}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}+\mathrm{1}} \\ $$$${such}\:{that}\:{a}_{{n}} \:{is}\:{maximum},\: \\ $$$$\frac{{a}_{{n}} }{{a}_{{n}−\mathrm{1}} }\geqslant\mathrm{1}: \\ $$$$\frac{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right)}{\left({n}+\mathrm{1}\right){n}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\geqslant\mathrm{1} \\ $$$$\frac{{n}+\mathrm{2}}{{n}}\geqslant\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{2}{n}+\mathrm{4}\geqslant\mathrm{3}{n} \\ $$$$\Rightarrow{n}\leqslant\mathrm{4} \\ $$$$\frac{{a}_{{n}} }{{a}_{{n}+\mathrm{1}} }\geqslant\mathrm{1}: \\ $$$$\frac{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right)}{\left({n}+\mathrm{3}\right)\left({n}+\mathrm{2}\right)}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{−\mathrm{1}} \geqslant\mathrm{1} \\ $$$$\frac{{n}+\mathrm{1}}{{n}+\mathrm{3}}\geqslant\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{3}{n}+\mathrm{3}\geqslant\mathrm{2}{n}+\mathrm{6} \\ $$$$\Rightarrow{n}\geqslant\mathrm{3} \\ $$$$\Rightarrow{n}=\mathrm{3}\:{or}\:\mathrm{4} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com