Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 116917 by I want to learn more last updated on 07/Oct/20

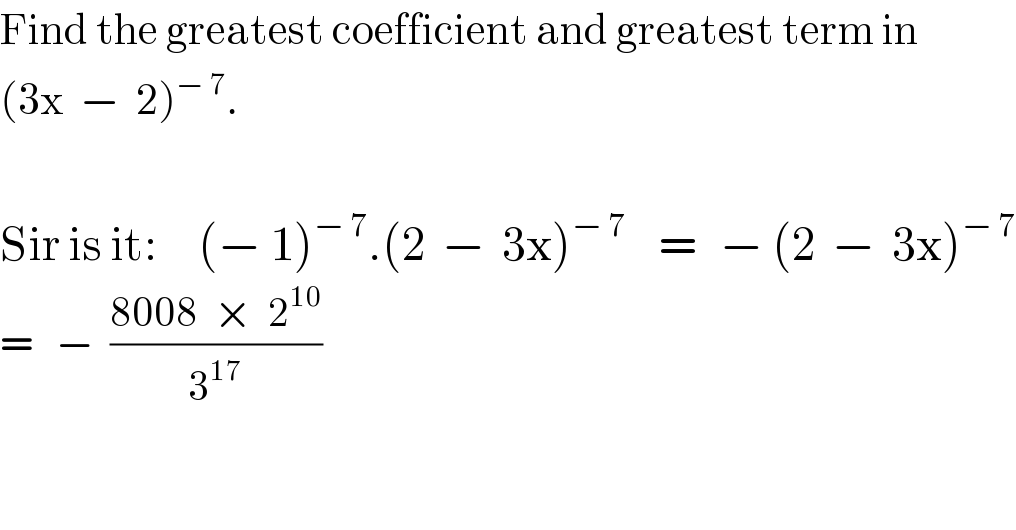
Find the greatest coefficient and greatest term in (3x − 2)^(− 7) . Sir is it: (− 1)^(− 7) .(2 − 3x)^(− 7) = − (2 − 3x)^(− 7) = − ((8008 × 2^(10) )/3^(17) )

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{coefficient}\:\mathrm{and}\:\mathrm{greatest}\:\mathrm{term}\:\mathrm{in} \\ $$$$\left(\mathrm{3x}\:\:−\:\:\mathrm{2}\right)^{−\:\mathrm{7}} . \\ $$$$ \\ $$$$\mathrm{Sir}\:\mathrm{is}\:\mathrm{it}:\:\:\:\:\:\left(−\:\mathrm{1}\right)^{−\:\mathrm{7}} .\left(\mathrm{2}\:\:−\:\:\mathrm{3x}\right)^{−\:\mathrm{7}} \:\:\:\:=\:\:\:−\:\left(\mathrm{2}\:\:−\:\:\mathrm{3x}\right)^{−\:\mathrm{7}} \\ $$$$=\:\:\:−\:\:\frac{\mathrm{8008}\:\:×\:\:\mathrm{2}^{\mathrm{10}} }{\mathrm{3}^{\mathrm{17}} } \\ $$

Answered by mr W last updated on 08/Oct/20

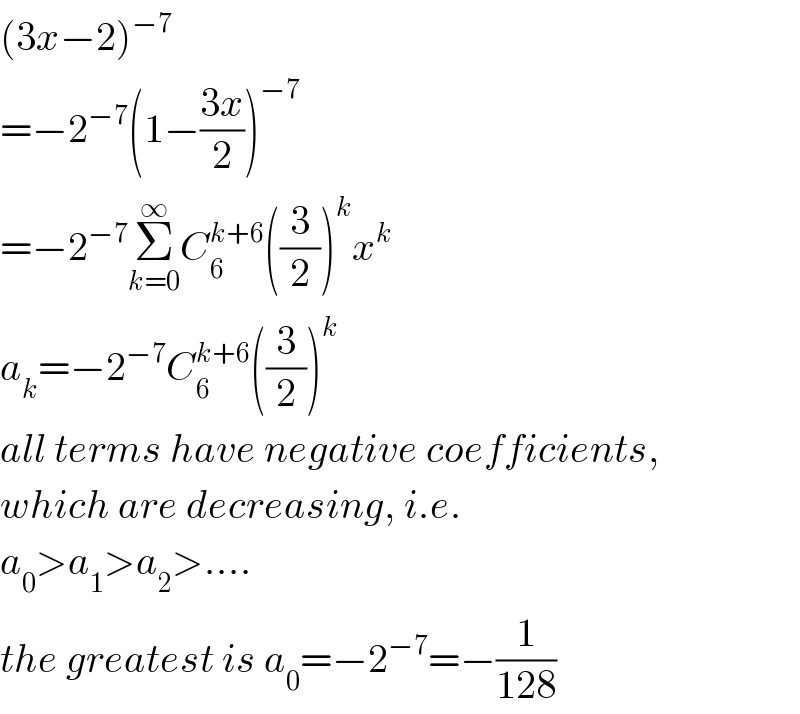
(3x−2)^(−7) =−2^(−7) (1−((3x)/2))^(−7) =−2^(−7) Σ_(k=0) ^∞ C_6 ^(k+6) ((3/2))^k x^k a_k =−2^(−7) C_6 ^(k+6) ((3/2))^k all terms have negative coefficients, which are decreasing, i.e. a_0 >a_1 >a_2 >.... the greatest is a_0 =−2^(−7) =−(1/(128))

$$\left(\mathrm{3}{x}−\mathrm{2}\right)^{−\mathrm{7}} \\ $$$$=−\mathrm{2}^{−\mathrm{7}} \left(\mathrm{1}−\frac{\mathrm{3}{x}}{\mathrm{2}}\right)^{−\mathrm{7}} \\ $$$$=−\mathrm{2}^{−\mathrm{7}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{6}} ^{{k}+\mathrm{6}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{k}} {x}^{{k}} \\ $$$${a}_{{k}} =−\mathrm{2}^{−\mathrm{7}} {C}_{\mathrm{6}} ^{{k}+\mathrm{6}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{k}} \\ $$$${all}\:{terms}\:{have}\:{negative}\:{coefficients}, \\ $$$${which}\:{are}\:{decreasing},\:{i}.{e}. \\ $$$${a}_{\mathrm{0}} >{a}_{\mathrm{1}} >{a}_{\mathrm{2}} >.... \\ $$$${the}\:{greatest}\:{is}\:{a}_{\mathrm{0}} =−\mathrm{2}^{−\mathrm{7}} =−\frac{\mathrm{1}}{\mathrm{128}} \\ $$

Commented by I want to learn more last updated on 08/Oct/20

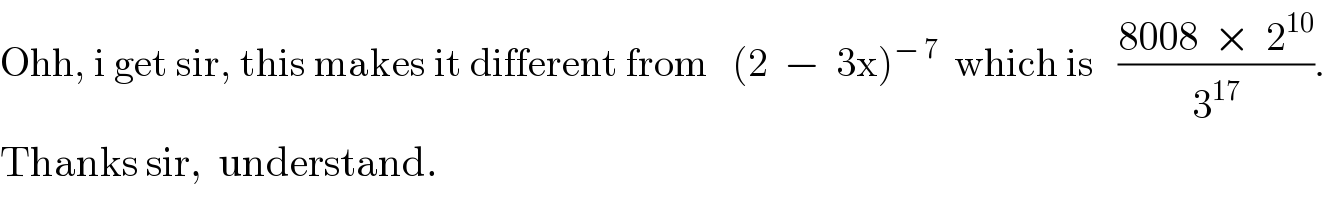
Ohh, i get sir, this makes it different from (2 − 3x)^(− 7) which is ((8008 × 2^(10) )/3^(17) ). Thanks sir, understand.

$$\mathrm{Ohh},\:\mathrm{i}\:\mathrm{get}\:\mathrm{sir},\:\mathrm{this}\:\mathrm{makes}\:\mathrm{it}\:\mathrm{different}\:\mathrm{from}\:\:\:\left(\mathrm{2}\:\:−\:\:\mathrm{3x}\right)^{−\:\mathrm{7}} \:\:\mathrm{which}\:\mathrm{is}\:\:\:\frac{\mathrm{8008}\:\:×\:\:\mathrm{2}^{\mathrm{10}} }{\mathrm{3}^{\mathrm{17}} }. \\ $$$$\mathrm{Thanks}\:\mathrm{sir},\:\:\mathrm{understand}. \\ $$

Commented by mr W last updated on 08/Oct/20

C_6 ^(k+6) ((2/3))^k has a maximum. C_6 ^(k+6) ((3/2))^k has no maximum.

$${C}_{\mathrm{6}} ^{{k}+\mathrm{6}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{k}} \:{has}\:{a}\:{maximum}. \\ $$$${C}_{\mathrm{6}} ^{{k}+\mathrm{6}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{k}} \:{has}\:{no}\:{maximum}. \\ $$

Commented by I want to learn more last updated on 08/Oct/20

I appreciate sir.

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com