Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 130894 by EDWIN88 last updated on 30/Jan/21

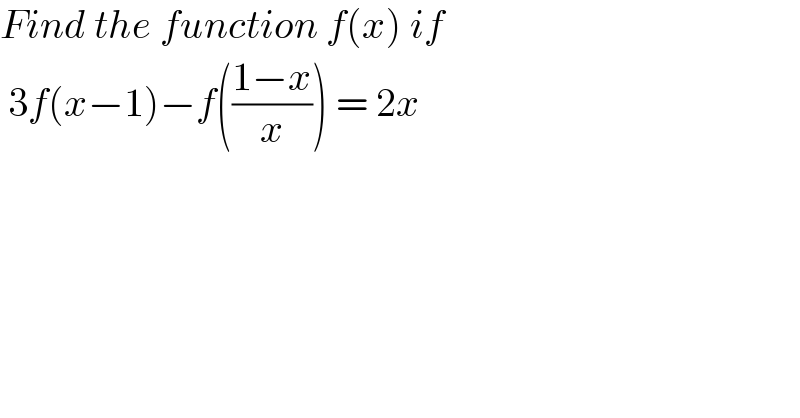
Find the function f(x) if 3f(x−1)−f(((1−x)/x)) = 2x

$${Find}\:{the}\:{function}\:{f}\left({x}\right)\:{if}\: \\ $$$$\:\mathrm{3}{f}\left({x}−\mathrm{1}\right)−{f}\left(\frac{\mathrm{1}−{x}}{{x}}\right)\:=\:\mathrm{2}{x}\: \\ $$

Commented by benjo_mathlover last updated on 30/Jan/21

այս հարցը շատ հետաքրքիր է

Commented by EDWIN88 last updated on 30/Jan/21

շնորհակալություն

Answered by mr W last updated on 30/Jan/21

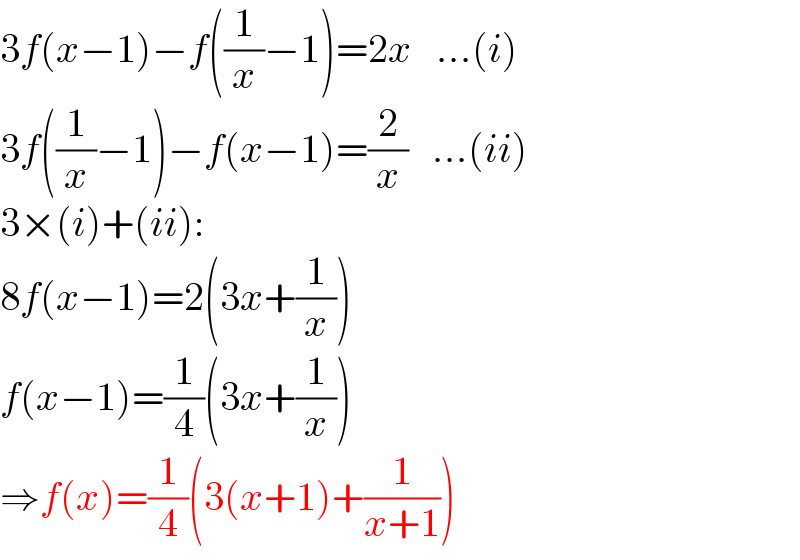
3f(x−1)−f((1/x)−1)=2x ...(i) 3f((1/x)−1)−f(x−1)=(2/x) ...(ii) 3×(i)+(ii): 8f(x−1)=2(3x+(1/x)) f(x−1)=(1/4)(3x+(1/x)) ⇒f(x)=(1/4)(3(x+1)+(1/(x+1)))

$$\mathrm{3}{f}\left({x}−\mathrm{1}\right)−{f}\left(\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)=\mathrm{2}{x}\:\:\:...\left({i}\right) \\ $$$$\mathrm{3}{f}\left(\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)−{f}\left({x}−\mathrm{1}\right)=\frac{\mathrm{2}}{{x}}\:\:\:...\left({ii}\right) \\ $$$$\mathrm{3}×\left({i}\right)+\left({ii}\right): \\ $$$$\mathrm{8}{f}\left({x}−\mathrm{1}\right)=\mathrm{2}\left(\mathrm{3}{x}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${f}\left({x}−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}{x}+\frac{\mathrm{1}}{{x}}\right) \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}\left({x}+\mathrm{1}\right)+\frac{\mathrm{1}}{{x}+\mathrm{1}}\right) \\ $$

Commented by EDWIN88 last updated on 30/Jan/21

����nice

Answered by benjo_mathlover last updated on 30/Jan/21

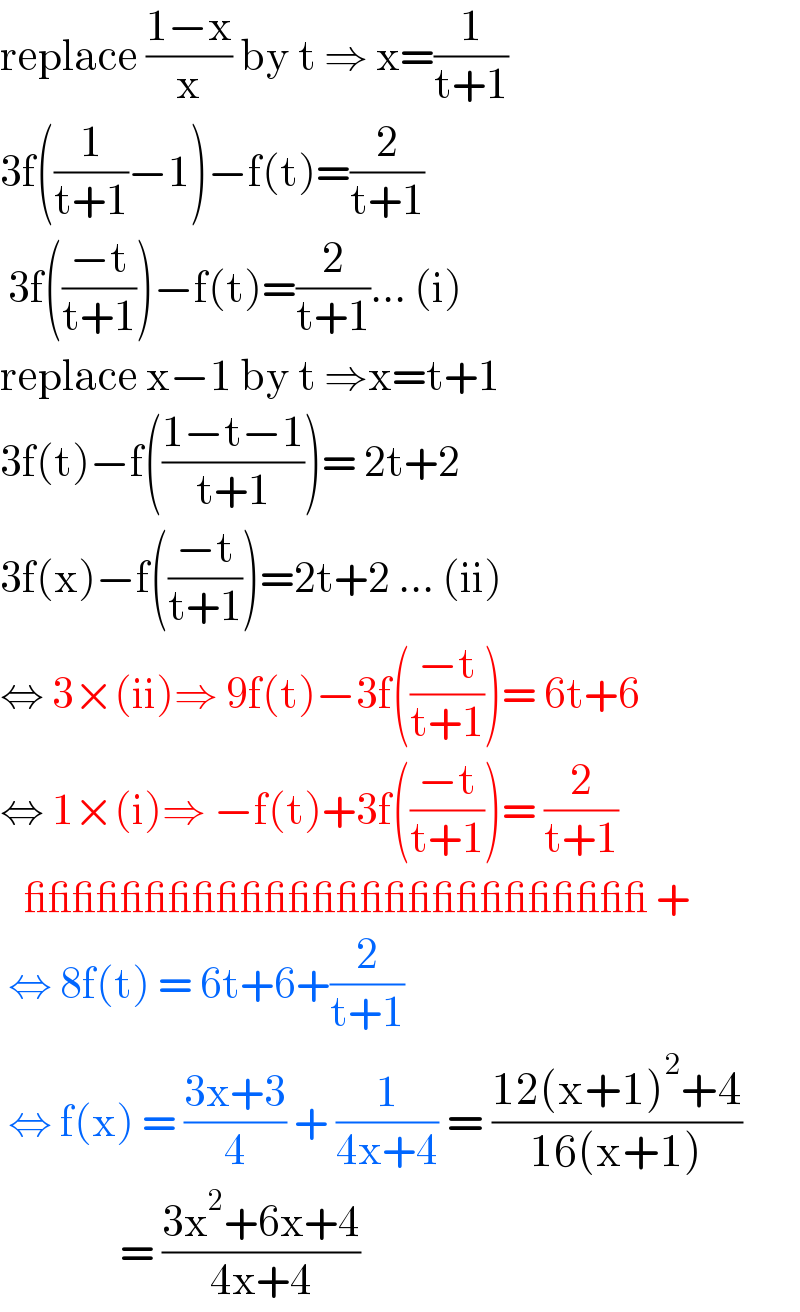
replace ((1−x)/x) by t ⇒ x=(1/(t+1)) 3f((1/(t+1))−1)−f(t)=(2/(t+1)) 3f(((−t)/(t+1)))−f(t)=(2/(t+1))... (i) replace x−1 by t ⇒x=t+1 3f(t)−f(((1−t−1)/(t+1)))= 2t+2 3f(x)−f(((−t)/(t+1)))=2t+2 ... (ii) ⇔ 3×(ii)⇒ 9f(t)−3f(((−t)/(t+1)))= 6t+6 ⇔ 1×(i)⇒ −f(t)+3f(((−t)/(t+1)))= (2/(t+1)) __________________________ + ⇔ 8f(t) = 6t+6+(2/(t+1)) ⇔ f(x) = ((3x+3)/4) + (1/(4x+4)) = ((12(x+1)^2 +4)/(16(x+1))) = ((3x^2 +6x+4)/(4x+4))

$$\mathrm{replace}\:\frac{\mathrm{1}−\mathrm{x}}{\mathrm{x}}\:\mathrm{by}\:\mathrm{t}\:\Rightarrow\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}} \\ $$$$\mathrm{3f}\left(\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}−\mathrm{1}\right)−\mathrm{f}\left(\mathrm{t}\right)=\frac{\mathrm{2}}{\mathrm{t}+\mathrm{1}} \\ $$$$\:\mathrm{3f}\left(\frac{−\mathrm{t}}{\mathrm{t}+\mathrm{1}}\right)−\mathrm{f}\left(\mathrm{t}\right)=\frac{\mathrm{2}}{\mathrm{t}+\mathrm{1}}...\:\left(\mathrm{i}\right) \\ $$$$\mathrm{replace}\:\mathrm{x}−\mathrm{1}\:\mathrm{by}\:\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{t}+\mathrm{1} \\ $$$$\mathrm{3f}\left(\mathrm{t}\right)−\mathrm{f}\left(\frac{\mathrm{1}−\mathrm{t}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)=\:\mathrm{2t}+\mathrm{2} \\ $$$$\mathrm{3f}\left(\mathrm{x}\right)−\mathrm{f}\left(\frac{−\mathrm{t}}{\mathrm{t}+\mathrm{1}}\right)=\mathrm{2t}+\mathrm{2}\:...\:\left(\mathrm{ii}\right) \\ $$$$\Leftrightarrow\:\mathrm{3}×\left(\mathrm{ii}\right)\Rightarrow\:\mathrm{9f}\left(\mathrm{t}\right)−\mathrm{3f}\left(\frac{−\mathrm{t}}{\mathrm{t}+\mathrm{1}}\right)=\:\mathrm{6t}+\mathrm{6} \\ $$$$\Leftrightarrow\:\mathrm{1}×\left(\mathrm{i}\right)\Rightarrow\:−\mathrm{f}\left(\mathrm{t}\right)+\mathrm{3f}\left(\frac{−\mathrm{t}}{\mathrm{t}+\mathrm{1}}\right)=\:\frac{\mathrm{2}}{\mathrm{t}+\mathrm{1}} \\ $$$$\:\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\:+ \\ $$$$\:\Leftrightarrow\:\mathrm{8f}\left(\mathrm{t}\right)\:=\:\mathrm{6t}+\mathrm{6}+\frac{\mathrm{2}}{\mathrm{t}+\mathrm{1}} \\ $$$$\:\Leftrightarrow\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{3x}+\mathrm{3}}{\mathrm{4}}\:+\:\frac{\mathrm{1}}{\mathrm{4x}+\mathrm{4}}\:=\:\frac{\mathrm{12}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}}{\mathrm{16}\left(\mathrm{x}+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{3x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{4}}{\mathrm{4x}+\mathrm{4}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com