Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 48291 by Rio Michael last updated on 21/Nov/18

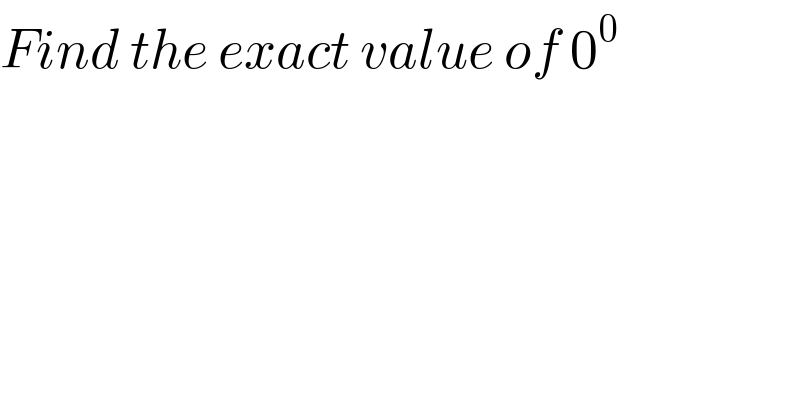
Find the exact value of 0^0

$${Find}\:{the}\:{exact}\:{value}\:{of}\:\mathrm{0}^{\mathrm{0}} \\ $$

Commented by maxmathsup by imad last updated on 21/Nov/18

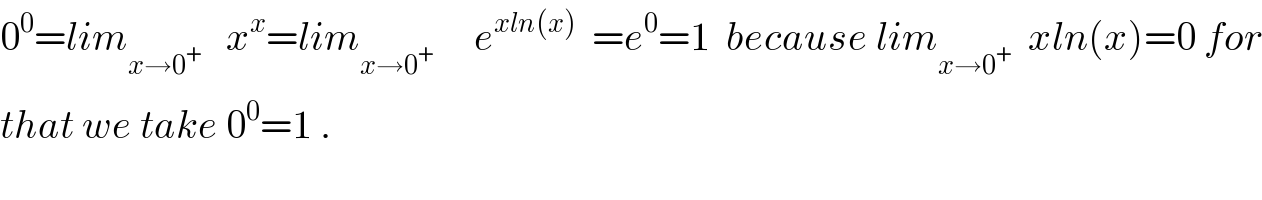
0^0 =lim_(x→0^+ ) x^x =lim_(x→0^+ ) e^(xln(x)) =e^0 =1 because lim_(x→0^+ ) xln(x)=0 for that we take 0^0 =1 .

$$\mathrm{0}^{\mathrm{0}} ={lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\:{x}^{{x}} ={lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\:\:\:{e}^{{xln}\left({x}\right)} \:\:={e}^{\mathrm{0}} =\mathrm{1}\:\:{because}\:{lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:{xln}\left({x}\right)=\mathrm{0}\:{for} \\ $$$${that}\:{we}\:{take}\:\mathrm{0}^{\mathrm{0}} =\mathrm{1}\:. \\ $$

Answered by MJS last updated on 21/Nov/18

0^0 is not defined 1^(st) step a÷b=(a/b)=c ⇒ a=c×b ⇒ b≠0 because if b=0 we have a÷0=(a/0)=c ⇒ a=c×0=0 example: 5÷0=(5/0)=c ⇒ 5=c×0=0 which is wrong conclusion: a÷0=(a/0) is not defined ⇒ ⇒ a÷b=(a/b)=c for b≠0 2^(nd) step a^n =a×a×a×... (n times) 0^n =0×0×0×... =0 (a^m /a^n )=a^(m−n) ⇒ (a^n /a^n )=a^0 =1 but because of our above conclusion a≠0 ⇒ 0^0 is not defined but sometimes it makes sense to define it for some reasons. in these cases we are free to set the value. f(x)=(x/x)=1 ∀x≠0 ⇒ we can define f(0)=1 to keep the function continous. or f(x)=x^x . usually we want to give it the value of the limit.

$$\mathrm{0}^{\mathrm{0}} \:\mathrm{is}\:\mathrm{not}\:\mathrm{defined} \\ $$$$\mathrm{1}^{\mathrm{st}} \:\mathrm{step} \\ $$$${a}\boldsymbol{\div}{b}=\frac{{a}}{{b}}={c}\:\Rightarrow\:{a}={c}×{b} \\ $$$$\Rightarrow\:{b}\neq\mathrm{0}\:\mathrm{because}\:\mathrm{if}\:{b}=\mathrm{0}\:\mathrm{we}\:\mathrm{have} \\ $$$${a}\boldsymbol{\div}\mathrm{0}=\frac{{a}}{\mathrm{0}}={c}\:\Rightarrow\:{a}={c}×\mathrm{0}=\mathrm{0} \\ $$$$\mathrm{example}:\:\mathrm{5}\boldsymbol{\div}\mathrm{0}=\frac{\mathrm{5}}{\mathrm{0}}={c}\:\Rightarrow\:\mathrm{5}={c}×\mathrm{0}=\mathrm{0}\:\mathrm{which}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\mathrm{conclusion}:\:{a}\boldsymbol{\div}\mathrm{0}=\frac{{a}}{\mathrm{0}}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\Rightarrow \\ $$$$\Rightarrow\:{a}\boldsymbol{\div}{b}=\frac{{a}}{{b}}={c}\:\mathrm{for}\:{b}\neq\mathrm{0} \\ $$$$ \\ $$$$\mathrm{2}^{\mathrm{nd}} \:\mathrm{step} \\ $$$${a}^{{n}} ={a}×{a}×{a}×...\:\left({n}\:\mathrm{times}\right) \\ $$$$\mathrm{0}^{{n}} =\mathrm{0}×\mathrm{0}×\mathrm{0}×...\:=\mathrm{0} \\ $$$$\frac{{a}^{{m}} }{{a}^{{n}} }={a}^{{m}−{n}} \:\Rightarrow\:\frac{{a}^{{n}} }{{a}^{{n}} }={a}^{\mathrm{0}} =\mathrm{1}\:\mathrm{but}\:\mathrm{because}\:\mathrm{of}\:\mathrm{our} \\ $$$$\mathrm{above}\:\mathrm{conclusion}\:{a}\neq\mathrm{0}\:\Rightarrow\:\mathrm{0}^{\mathrm{0}} \:\mathrm{is}\:\mathrm{not}\:\mathrm{defined} \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{sometimes}\:\mathrm{it}\:\mathrm{makes}\:\mathrm{sense}\:\mathrm{to}\:\mathrm{define}\:\mathrm{it} \\ $$$$\mathrm{for}\:\mathrm{some}\:\mathrm{reasons}.\:\mathrm{in}\:\mathrm{these}\:\mathrm{cases}\:\mathrm{we}\:\mathrm{are}\:\mathrm{free} \\ $$$$\mathrm{to}\:\mathrm{set}\:\mathrm{the}\:\mathrm{value}.\:{f}\left({x}\right)=\frac{{x}}{{x}}=\mathrm{1}\:\forall{x}\neq\mathrm{0}\:\Rightarrow\:\mathrm{we} \\ $$$$\mathrm{can}\:\mathrm{define}\:{f}\left(\mathrm{0}\right)=\mathrm{1}\:\mathrm{to}\:\mathrm{keep}\:\mathrm{the}\:\mathrm{function} \\ $$$$\mathrm{continous}.\:\mathrm{or}\:{f}\left({x}\right)={x}^{{x}} .\:\mathrm{usually}\:\mathrm{we}\:\mathrm{want}\:\mathrm{to} \\ $$$$\mathrm{give}\:\mathrm{it}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{limit}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com