
Question Number 187255 by Spillover last updated on 15/Feb/23
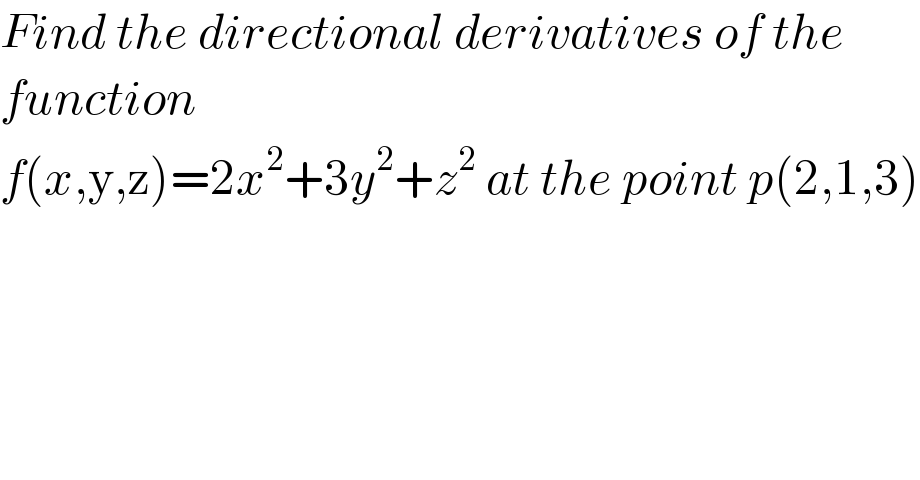
$${Find}\:{the}\:{directional}\:{derivatives}\:{of}\:{the} \\ $$$${function}\: \\ $$$${f}\left({x},\mathrm{y},\mathrm{z}\right)=\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:{at}\:{the}\:{point}\:{p}\left(\mathrm{2},\mathrm{1},\mathrm{3}\right) \\ $$
Answered by MikeH last updated on 15/Feb/23
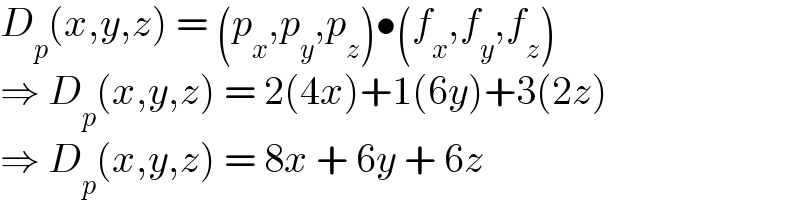
$${D}_{{p}} \left({x},{y},{z}\right)\:=\:\left({p}_{{x}} ,{p}_{{y}} ,{p}_{{z}} \right)\bullet\left({f}_{{x}} ,{f}_{{y}} ,{f}_{{z}} \right) \\ $$$$\Rightarrow\:{D}_{{p}} \left({x},{y},{z}\right)\:=\:\mathrm{2}\left(\mathrm{4}{x}\right)+\mathrm{1}\left(\mathrm{6}{y}\right)+\mathrm{3}\left(\mathrm{2}{z}\right) \\ $$$$\Rightarrow\:{D}_{{p}} \left({x},{y},{z}\right)\:=\:\mathrm{8}{x}\:+\:\mathrm{6}{y}\:+\:\mathrm{6}{z} \\ $$
