Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 200460 by deleteduser12 last updated on 19/Nov/23

Find the cardano′s solution of the equation 28x^3 −9x^2 +1=0

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{cardano}'\mathrm{s}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{equation}\:\mathrm{28x}^{\mathrm{3}} −\mathrm{9x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$

Answered by Frix last updated on 19/Nov/23

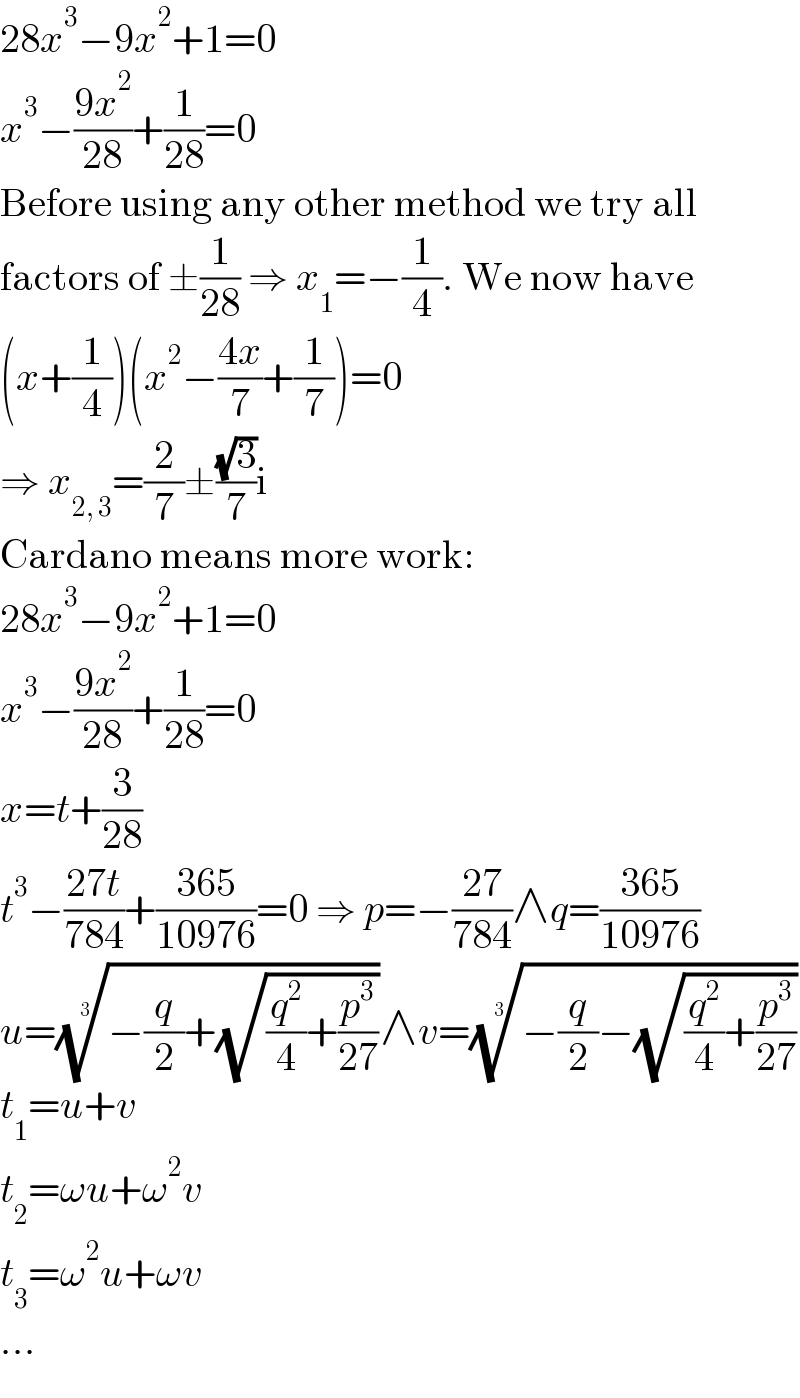
28x^3 −9x^2 +1=0 x^3 −((9x^2 )/(28))+(1/(28))=0 Before using any other method we try all factors of ±(1/(28)) ⇒ x_1 =−(1/4). We now have (x+(1/4))(x^2 −((4x)/7)+(1/7))=0 ⇒ x_(2, 3) =(2/7)±((√3)/7)i Cardano means more work: 28x^3 −9x^2 +1=0 x^3 −((9x^2 )/(28))+(1/(28))=0 x=t+(3/(28)) t^3 −((27t)/(784))+((365)/(10976))=0 ⇒ p=−((27)/(784))∧q=((365)/(10976)) u=((−(q/2)+(√((q^2 /4)+(p^3 /(27))))))^(1/3) ∧v=((−(q/2)−(√((q^2 /4)+(p^3 /(27))))))^(1/3) t_1 =u+v t_2 =ωu+ω^2 v t_3 =ω^2 u+ωv ...

$$\mathrm{28}{x}^{\mathrm{3}} −\mathrm{9}{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{28}}+\frac{\mathrm{1}}{\mathrm{28}}=\mathrm{0} \\ $$$$\mathrm{Before}\:\mathrm{using}\:\mathrm{any}\:\mathrm{other}\:\mathrm{method}\:\mathrm{we}\:\mathrm{try}\:\mathrm{all} \\ $$$$\mathrm{factors}\:\mathrm{of}\:\pm\frac{\mathrm{1}}{\mathrm{28}}\:\Rightarrow\:{x}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{4}}.\:\mathrm{We}\:\mathrm{now}\:\mathrm{have} \\ $$$$\left({x}+\frac{\mathrm{1}}{\mathrm{4}}\right)\left({x}^{\mathrm{2}} −\frac{\mathrm{4}{x}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{7}}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{x}_{\mathrm{2},\:\mathrm{3}} =\frac{\mathrm{2}}{\mathrm{7}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{7}}\mathrm{i} \\ $$$$\mathrm{Cardano}\:\mathrm{means}\:\mathrm{more}\:\mathrm{work}: \\ $$$$\mathrm{28}{x}^{\mathrm{3}} −\mathrm{9}{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{28}}+\frac{\mathrm{1}}{\mathrm{28}}=\mathrm{0} \\ $$$${x}={t}+\frac{\mathrm{3}}{\mathrm{28}} \\ $$$${t}^{\mathrm{3}} −\frac{\mathrm{27}{t}}{\mathrm{784}}+\frac{\mathrm{365}}{\mathrm{10976}}=\mathrm{0}\:\Rightarrow\:{p}=−\frac{\mathrm{27}}{\mathrm{784}}\wedge{q}=\frac{\mathrm{365}}{\mathrm{10976}} \\ $$$${u}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}}\wedge{v}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}−\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}} \\ $$$${t}_{\mathrm{1}} ={u}+{v} \\ $$$${t}_{\mathrm{2}} =\omega{u}+\omega^{\mathrm{2}} {v} \\ $$$${t}_{\mathrm{3}} =\omega^{\mathrm{2}} {u}+\omega{v} \\ $$$$... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com