
Question Number 210917 by depressiveshrek last updated on 22/Aug/24

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{intersected}\:\mathrm{by}\:\mathrm{three} \\ $$$$\mathrm{circles}\:\mathrm{of}\:\mathrm{radius}\:\mathrm{1},\:\mathrm{centered}\:\mathrm{at}\:\mathrm{the} \\ $$$$\mathrm{origin},\:\mathrm{at}\:\left(\mathrm{1},\:\mathrm{0}\right)\:\mathrm{and}\:\left(\mathrm{1},\:\mathrm{1}\right)\:\mathrm{respectively}. \\ $$
Answered by mr W last updated on 22/Aug/24
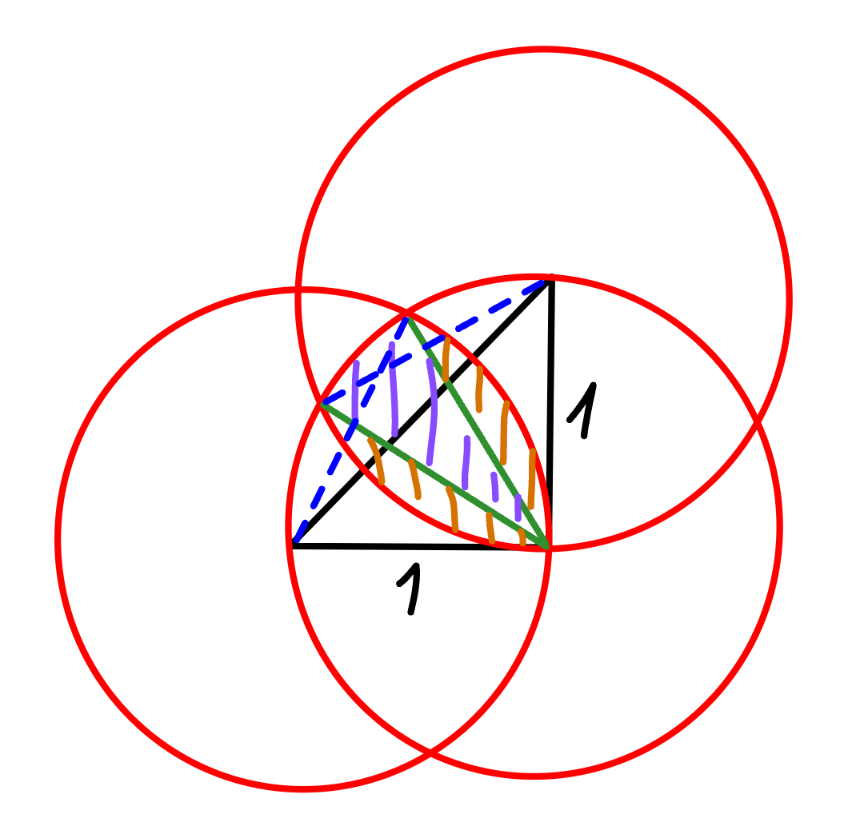
Commented by mr W last updated on 22/Aug/24
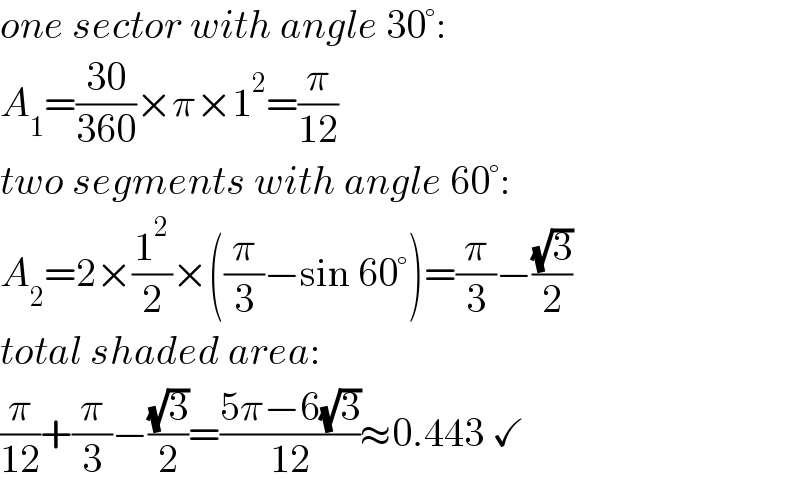
$${one}\:{sector}\:{with}\:{angle}\:\mathrm{30}°: \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{30}}{\mathrm{360}}×\pi×\mathrm{1}^{\mathrm{2}} =\frac{\pi}{\mathrm{12}} \\ $$$${two}\:{segments}\:{with}\:{angle}\:\mathrm{60}°: \\ $$$${A}_{\mathrm{2}} =\mathrm{2}×\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{2}}×\left(\frac{\pi}{\mathrm{3}}−\mathrm{sin}\:\mathrm{60}°\right)=\frac{\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${total}\:{shaded}\:{area}: \\ $$$$\frac{\pi}{\mathrm{12}}+\frac{\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{5}\pi−\mathrm{6}\sqrt{\mathrm{3}}}{\mathrm{12}}\approx\mathrm{0}.\mathrm{443}\:\checkmark \\ $$
