
Question Number 140615 by bramlexs22 last updated on 10/May/21
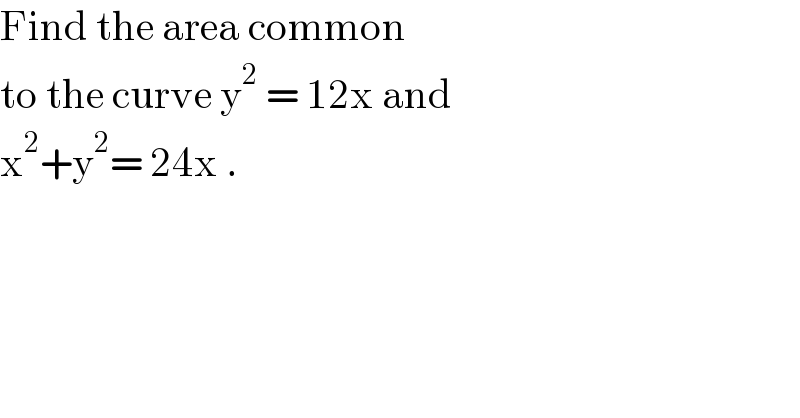
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{common}\: \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{12x}\:\mathrm{and} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\:\mathrm{24x}\:. \\ $$
Answered by EDWIN88 last updated on 10/May/21
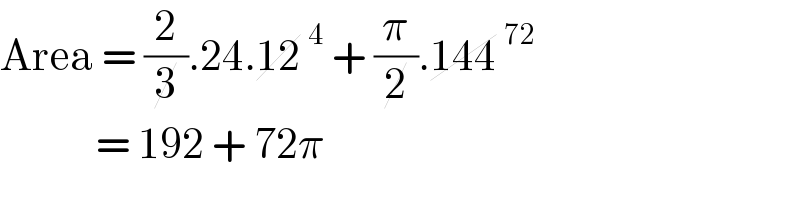
$$\mathrm{Area}\:=\:\frac{\mathrm{2}}{\cancel{\mathrm{3}}}.\mathrm{24}.\cancel{\mathrm{12}}\:^{\mathrm{4}} \:+\:\frac{\pi}{\cancel{\mathrm{2}}}.\cancel{\mathrm{144}}\:^{\mathrm{72}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{192}\:+\:\mathrm{72}\pi \\ $$
Commented by EDWIN88 last updated on 10/May/21
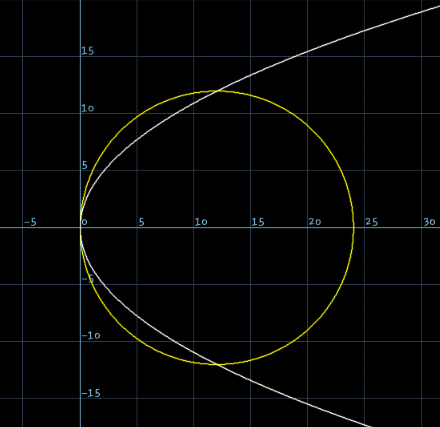
Commented by Dwaipayan Shikari last updated on 10/May/21
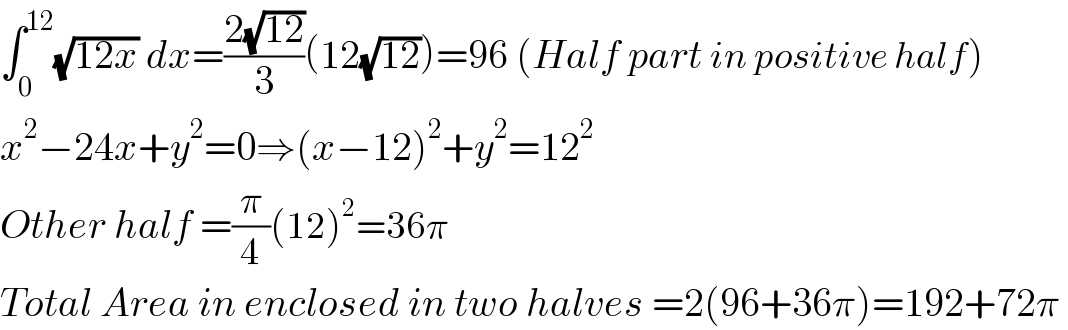
$$\int_{\mathrm{0}} ^{\mathrm{12}} \sqrt{\mathrm{12}{x}}\:{dx}=\frac{\mathrm{2}\sqrt{\mathrm{12}}}{\mathrm{3}}\left(\mathrm{12}\sqrt{\mathrm{12}}\right)=\mathrm{96}\:\left({Half}\:{part}\:{in}\:{positive}\:{half}\right) \\ $$$${x}^{\mathrm{2}} −\mathrm{24}{x}+{y}^{\mathrm{2}} =\mathrm{0}\Rightarrow\left({x}−\mathrm{12}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{12}^{\mathrm{2}} \\ $$$${Other}\:{half}\:=\frac{\pi}{\mathrm{4}}\left(\mathrm{12}\right)^{\mathrm{2}} =\mathrm{36}\pi \\ $$$${Total}\:{Area}\:{in}\:{enclosed}\:{in}\:{two}\:{halves}\:=\mathrm{2}\left(\mathrm{96}+\mathrm{36}\pi\right)=\mathrm{192}+\mathrm{72}\pi\: \\ $$
