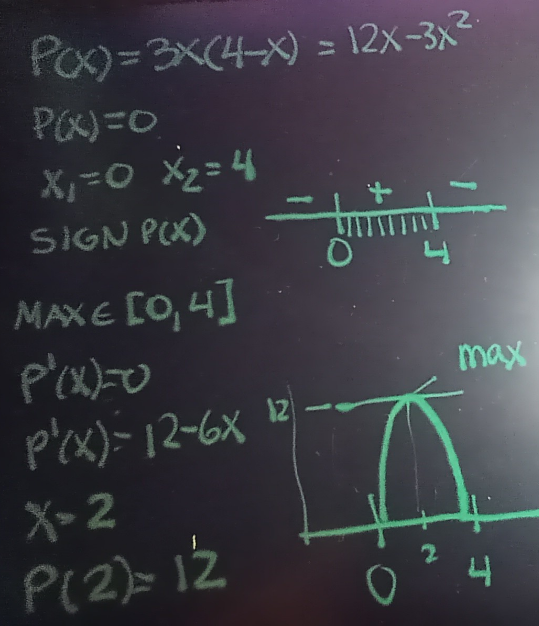Question Number 183464 by Mastermind last updated on 26/Dec/22
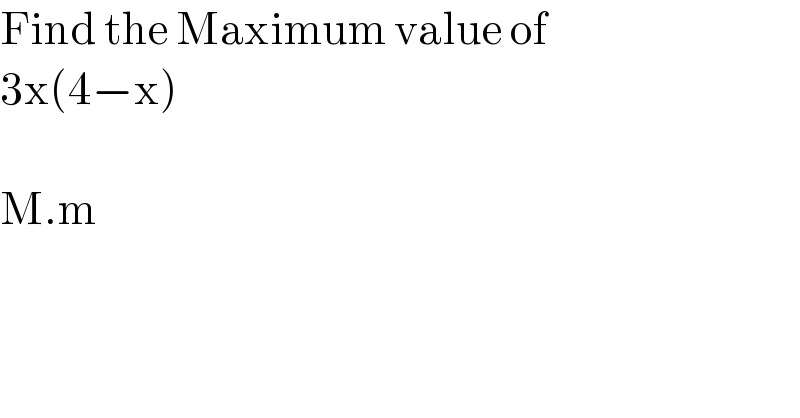
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{Maximum}\:\mathrm{value}\:\mathrm{of} \\ $$$$\mathrm{3x}\left(\mathrm{4}−\mathrm{x}\right) \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$
Answered by mr W last updated on 26/Dec/22
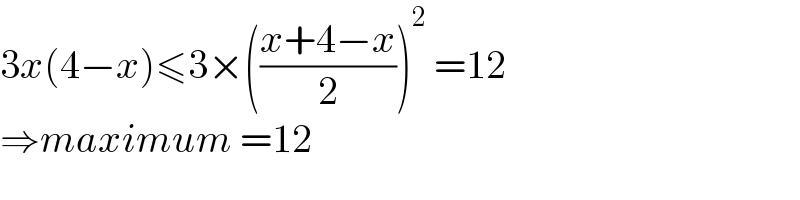
$$\mathrm{3}{x}\left(\mathrm{4}−{x}\right)\leqslant\mathrm{3}×\left(\frac{{x}+\mathrm{4}−{x}}{\mathrm{2}}\right)^{\mathrm{2}} \:=\mathrm{12} \\ $$$$\Rightarrow{maximum}\:=\mathrm{12} \\ $$
Commented by manolex last updated on 26/Dec/22
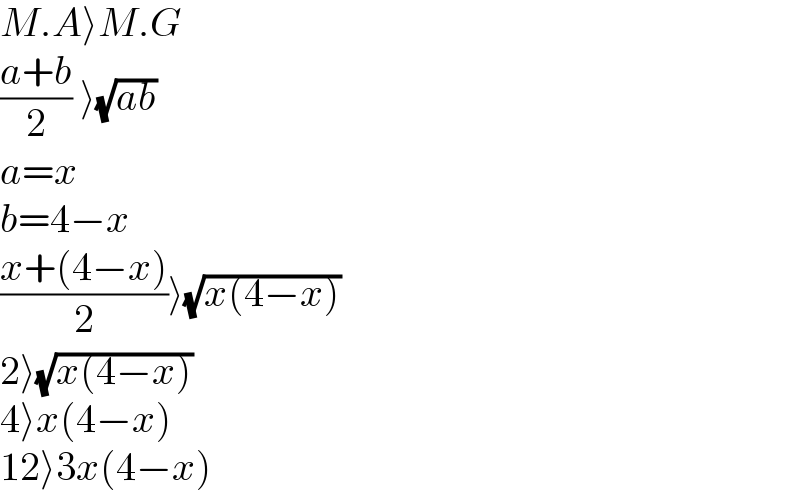
$${M}.{A}\rangle{M}.{G} \\ $$$$\frac{{a}+{b}}{\mathrm{2}}\:\rangle\sqrt{{ab}} \\ $$$${a}={x} \\ $$$${b}=\mathrm{4}−{x} \\ $$$$\frac{{x}+\left(\mathrm{4}−{x}\right)}{\mathrm{2}}\rangle\sqrt{{x}\left(\mathrm{4}−{x}\right)} \\ $$$$\mathrm{2}\rangle\sqrt{{x}\left(\mathrm{4}−{x}\right)} \\ $$$$\mathrm{4}\rangle{x}\left(\mathrm{4}−{x}\right) \\ $$$$\mathrm{12}\rangle\mathrm{3}{x}\left(\mathrm{4}−{x}\right) \\ $$
Answered by manxsol last updated on 26/Dec/22