
Question Number 140330 by Satyendra last updated on 06/May/21
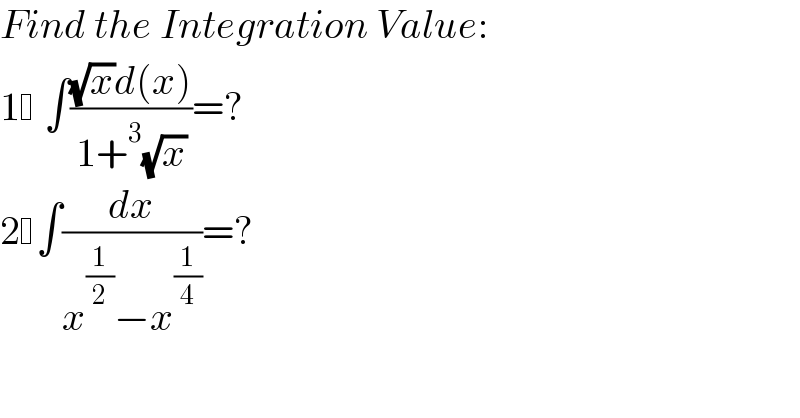
$${Find}\:{the}\:{Integration}\:{Value}: \\ $$$$\mathrm{1} \:\int\frac{\sqrt{{x}}{d}\left({x}\right)}{\mathrm{1}+^{\mathrm{3}} \sqrt{{x}}}=? \\ $$$$\mathrm{2} \int\frac{{dx}}{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} −{x}^{\frac{\mathrm{1}}{\mathrm{4}}} }=? \\ $$
Answered by john_santu last updated on 06/May/21
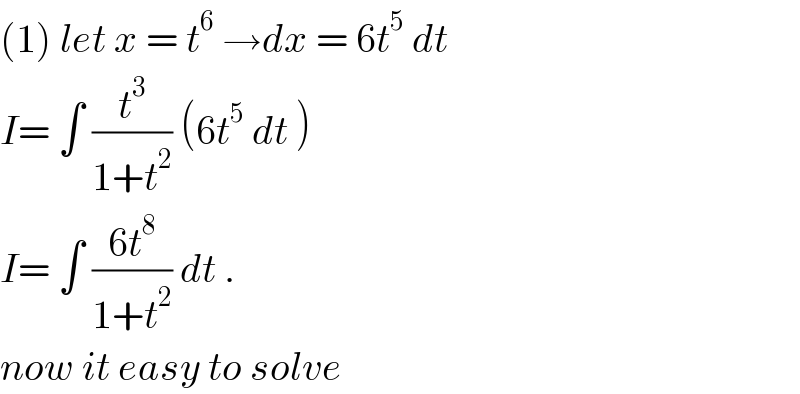
$$\left(\mathrm{1}\right)\:{let}\:{x}\:=\:{t}^{\mathrm{6}} \:\rightarrow{dx}\:=\:\mathrm{6}{t}^{\mathrm{5}} \:{dt} \\ $$$${I}=\:\int\:\frac{{t}^{\mathrm{3}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:\left(\mathrm{6}{t}^{\mathrm{5}} \:{dt}\:\right) \\ $$$${I}=\:\int\:\frac{\mathrm{6}{t}^{\mathrm{8}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:. \\ $$$${now}\:{it}\:{easy}\:{to}\:{solve} \\ $$
Answered by benjo_mathlover last updated on 06/May/21
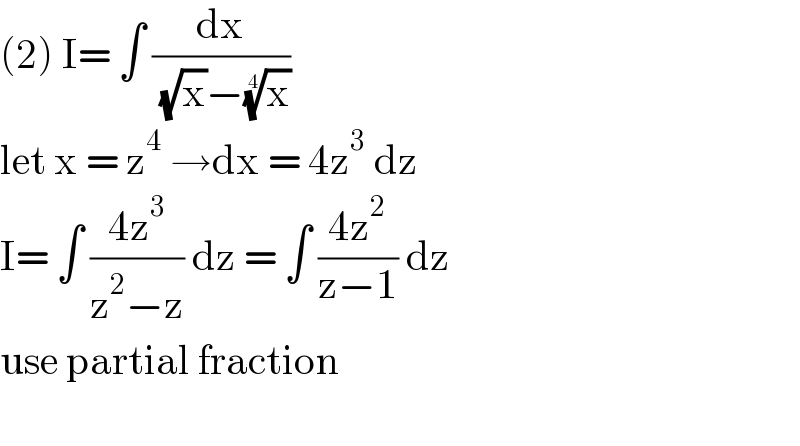
$$\left(\mathrm{2}\right)\:\mathrm{I}=\:\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}}−\sqrt[{\mathrm{4}}]{\mathrm{x}}}\: \\ $$$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{z}^{\mathrm{4}} \:\rightarrow\mathrm{dx}\:=\:\mathrm{4z}^{\mathrm{3}} \:\mathrm{dz} \\ $$$$\mathrm{I}=\:\int\:\frac{\mathrm{4z}^{\mathrm{3}} }{\mathrm{z}^{\mathrm{2}} −\mathrm{z}}\:\mathrm{dz}\:=\:\int\:\frac{\mathrm{4z}^{\mathrm{2}} }{\mathrm{z}−\mathrm{1}}\:\mathrm{dz}\: \\ $$$$\mathrm{use}\:\mathrm{partial}\:\mathrm{fraction} \\ $$$$ \\ $$
