Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 202306 by hardmath last updated on 24/Dec/23

Find the 2023rd term in the sequence 2,3,5,6,7,8,10,11,12,13,14,15,17,18,... obtained by subtracting integer squares from natural numbers.

$$ \\ $$Find the 2023rd term in the sequence 2,3,5,6,7,8,10,11,12,13,14,15,17,18,... obtained by subtracting integer squares from natural numbers.

Answered by deleteduser1 last updated on 24/Dec/23

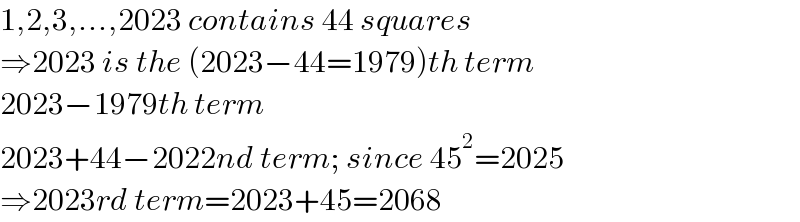
1,2,3,...,2023 contains 44 squares ⇒2023 is the (2023−44=1979)th term 2023−1979th term 2023+44−2022nd term; since 45^2 =2025 ⇒2023rd term=2023+45=2068

$$\mathrm{1},\mathrm{2},\mathrm{3},...,\mathrm{2023}\:{contains}\:\mathrm{44}\:{squares} \\ $$$$\Rightarrow\mathrm{2023}\:{is}\:{the}\:\left(\mathrm{2023}−\mathrm{44}=\mathrm{1979}\right){th}\:{term} \\ $$$$\mathrm{2023}−\mathrm{1979}{th}\:{term} \\ $$$$\mathrm{2023}+\mathrm{44}−\mathrm{2022}{nd}\:{term};\:{since}\:\mathrm{45}^{\mathrm{2}} =\mathrm{2025} \\ $$$$\Rightarrow\mathrm{2023}{rd}\:{term}=\mathrm{2023}+\mathrm{45}=\mathrm{2068} \\ $$

Commented by hardmath last updated on 24/Dec/23

thank you dear professor

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor} \\ $$

Answered by mr W last updated on 24/Dec/23

1,2,3,4,5,...,n 1^2 ,2^2 ,3^2 ,...,k^2 with k^2 <n, i.e. k=⌊(√n)⌋ m=n−k=n−⌊(√n)⌋ that means the m^(th) term is n. ⌊(√n)⌋≤(√n) m=n−⌊(√n)⌋≥n−(√n) n−(√n)−m≤0 ⇒(√n)≤((1+(√(1+4m)))/2) ⇒n≤((((√(4m+1))+1)^2 )/4) i.e. the m^(th) term is a_m =⌊((((√(4m+1))+1)^2 )/4)⌋ examples: m=2023: a_(2023) =⌊((((√(4×2023+1))+1)^2 )/4)⌋=2068 m=2025: a_(2025) =⌊((((√(4×2025+1))+1)^2 )/4)⌋=2070 m=1000: a_(1000) =⌊((((√(4×1000+1))+1)^2 )/4)⌋=1032 m=3000: a_(3000) =⌊((((√(4×3000+1))+1)^2 )/4)⌋=3055

$$\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},...,{n} \\ $$$$\mathrm{1}^{\mathrm{2}} ,\mathrm{2}^{\mathrm{2}} ,\mathrm{3}^{\mathrm{2}} ,...,{k}^{\mathrm{2}} \:{with}\:{k}^{\mathrm{2}} <{n},\:{i}.{e}.\:{k}=\lfloor\sqrt{{n}}\rfloor \\ $$$${m}={n}−{k}={n}−\lfloor\sqrt{{n}}\rfloor \\ $$$${that}\:{means}\:{the}\:{m}^{{th}} \:{term}\:{is}\:{n}. \\ $$$$\lfloor\sqrt{{n}}\rfloor\leqslant\sqrt{{n}} \\ $$$${m}={n}−\lfloor\sqrt{{n}}\rfloor\geqslant{n}−\sqrt{{n}} \\ $$$${n}−\sqrt{{n}}−{m}\leqslant\mathrm{0} \\ $$$$\Rightarrow\sqrt{{n}}\leqslant\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{m}}}{\mathrm{2}}\: \\ $$$$\Rightarrow{n}\leqslant\frac{\left(\sqrt{\mathrm{4}{m}+\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$${i}.{e}.\:{the}\:{m}^{{th}} \:{term}\:{is} \\ $$$${a}_{{m}} =\lfloor\frac{\left(\sqrt{\mathrm{4}{m}+\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\rfloor \\ $$$${examples}: \\ $$$${m}=\mathrm{2023}:\: \\ $$$$\:\:\:{a}_{\mathrm{2023}} =\lfloor\frac{\left(\sqrt{\mathrm{4}×\mathrm{2023}+\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\rfloor=\mathrm{2068} \\ $$$${m}=\mathrm{2025}:\: \\ $$$$\:\:\:{a}_{\mathrm{2025}} =\lfloor\frac{\left(\sqrt{\mathrm{4}×\mathrm{2025}+\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\rfloor=\mathrm{2070} \\ $$$${m}=\mathrm{1000}: \\ $$$$\:\:\:{a}_{\mathrm{1000}} =\lfloor\frac{\left(\sqrt{\mathrm{4}×\mathrm{1000}+\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\rfloor=\mathrm{1032} \\ $$$${m}=\mathrm{3000}: \\ $$$$\:\:\:{a}_{\mathrm{3000}} =\lfloor\frac{\left(\sqrt{\mathrm{4}×\mathrm{3000}+\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\rfloor=\mathrm{3055} \\ $$

Commented by hardmath last updated on 24/Dec/23

perfect solution tahnkyou dear professor

$$\mathrm{perfect}\:\mathrm{solution}\:\mathrm{tahnkyou}\:\mathrm{dear}\:\mathrm{professor} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com