
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 125768 by Don08q last updated on 13/Dec/20
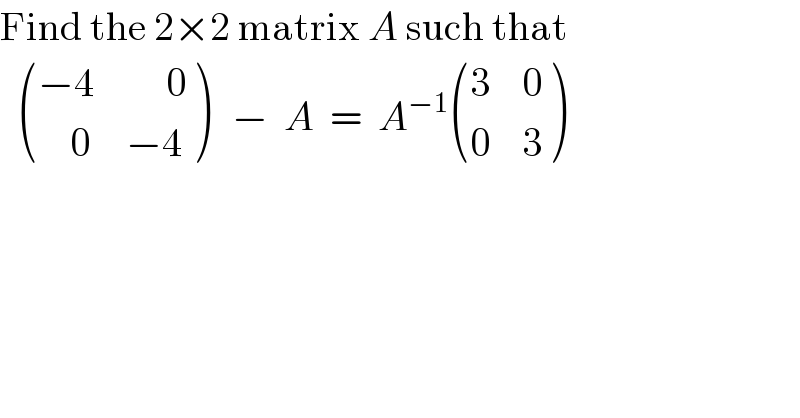
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{2}×\mathrm{2}\:\mathrm{matrix}\:{A}\:\mathrm{such}\:\mathrm{that} \\ $$$$\:\:\begin{pmatrix}{−\mathrm{4}}&{\:\:\:\:\:\mathrm{0}}\\{\:\:\:\:\mathrm{0}}&{−\mathrm{4}}\end{pmatrix}\:\:\:−\:\:{A}\:\:=\:\:{A}^{−\mathrm{1}} \begin{pmatrix}{\mathrm{3}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{3}}\end{pmatrix} \\ $$
Answered by 676597498 last updated on 13/Dec/20
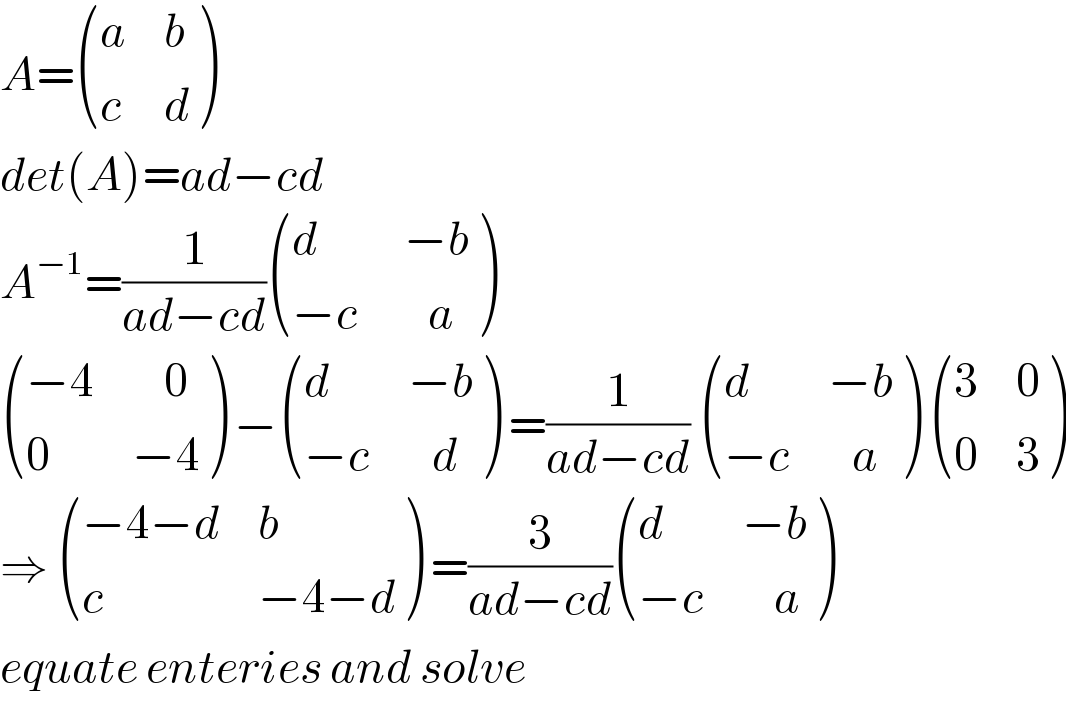
$${A}=\begin{pmatrix}{{a}}&{{b}}\\{{c}}&{{d}}\end{pmatrix}\: \\ $$$${det}\left({A}\right)={ad}−{cd} \\ $$$${A}^{−\mathrm{1}} =\frac{\mathrm{1}}{{ad}−{cd}}\begin{pmatrix}{{d}}&{−{b}}\\{−{c}\:}&{\:\:\:{a}}\end{pmatrix} \\ $$$$\begin{pmatrix}{−\mathrm{4}}&{\:\:\:\:\mathrm{0}}\\{\mathrm{0}}&{−\mathrm{4}}\end{pmatrix}\:−\begin{pmatrix}{{d}}&{−{b}}\\{−{c}}&{\:\:\:{d}}\end{pmatrix}\:=\frac{\mathrm{1}}{{ad}−{cd}}\:\begin{pmatrix}{{d}}&{−{b}}\\{−{c}}&{\:\:\:{a}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{3}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{3}}\end{pmatrix} \\ $$$$\Rightarrow\:\begin{pmatrix}{−\mathrm{4}−{d}}&{{b}}\\{{c}}&{−\mathrm{4}−{d}}\end{pmatrix}\:=\frac{\mathrm{3}}{{ad}−{cd}}\begin{pmatrix}{{d}}&{−{b}}\\{−{c}}&{\:\:\:\:{a}}\end{pmatrix} \\ $$$${equate}\:{enteries}\:{and}\:{solve} \\ $$
Answered by Olaf last updated on 13/Dec/20
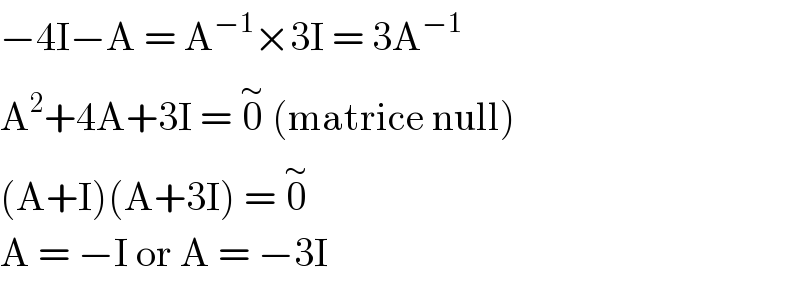
$$−\mathrm{4I}−\mathrm{A}\:=\:\mathrm{A}^{−\mathrm{1}} ×\mathrm{3I}\:=\:\mathrm{3A}^{−\mathrm{1}} \\ $$$$\mathrm{A}^{\mathrm{2}} +\mathrm{4A}+\mathrm{3I}\:=\:\overset{\sim} {\mathrm{0}}\:\left(\mathrm{matrice}\:\mathrm{null}\right) \\ $$$$\left(\mathrm{A}+\mathrm{I}\right)\left(\mathrm{A}+\mathrm{3I}\right)\:=\:\overset{\sim} {\mathrm{0}} \\ $$$$\mathrm{A}\:=\:−\mathrm{I}\:\mathrm{or}\:\mathrm{A}\:=\:−\mathrm{3I} \\ $$
Commented by mindispower last updated on 13/Dec/20

$${AM}=\mathrm{0}\nRightarrow{A}=\mathrm{0}\:{or}\:{M}=\mathrm{0} \\ $$$$\begin{pmatrix}{\mathrm{0}\:\:\:\:\mathrm{0}}\\{\mathrm{1}\:\:\:\:\mathrm{0}}\end{pmatrix}.\begin{pmatrix}{\mathrm{0}\:\:\:\:\mathrm{0}}\\{\mathrm{1}\:\:\:\:\mathrm{0}\:\:\:\:\:}\end{pmatrix}=\mathrm{0} \\ $$
Commented by Olaf last updated on 14/Dec/20

$$\mathrm{Sure}\:\mathrm{sir}\:\mathrm{but}\:\mathrm{in}\:\mathrm{your}\:\mathrm{example} \\ $$$$\mathrm{the}\:\mathrm{determinant}\:\mathrm{of}\:\mathrm{A}\:\mathrm{and}\:\mathrm{M}\:\mathrm{are}\:\mathrm{0}. \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{not}\:\mathrm{the}\:\mathrm{case}\:\mathrm{in}\:\mathrm{the}\:\mathrm{exercise}\:\mathrm{and}\:\mathrm{we} \\ $$$$\mathrm{verify}\:\mathrm{that}\:\mathrm{the}\:\mathrm{two}\:\mathrm{solutions}\:\mathrm{found} \\ $$$$\mathrm{are}\:\mathrm{really}\:\mathrm{solutions}...\:\mathrm{of}\:\mathrm{course}. \\ $$
Answered by liberty last updated on 13/Dec/20
![(((a b)),((c d)) ) [ (((−4 0)),(( 0 −4)) )− (((a b)),((c d)) ) ] = (((3 0)),((0 3)) ) (((a b)),((c d)) ) (((−4−a − b)),(( −c −4−d)) ) = (((3 0)),((0 3)) ) (((−a^2 −4a−bc −ab−4b−bd)),((−ac−4c−cd −bc−4d−d^2 )) ) = (((3 0)),((0 3)) ) (•) −ab−4b−bd=0 ; b(a+4+d)=0 → { ((b=0)),((a+d=−4)) :} (••)−ac−4c−cd=0 ; c(a+d+4)=0→ { ((c=0)),((a+d=−4)) :} for b=0 ⇒−a^2 −4a=3 ; a^2 +4a+3=0 (a+1)(a+3)=0→ { ((a=−1 ∧d=−3)),((a=−3 ∧d=−1)) :} A= (((−1 0)),(( 0 −3)) ) or A= (((−3 0)),(( 0 −1)) )](Q125795.png)
$$\begin{pmatrix}{{a}\:\:\:\:{b}}\\{{c}\:\:\:\:{d}}\end{pmatrix}\:\left[\:\begin{pmatrix}{−\mathrm{4}\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:\:−\mathrm{4}}\end{pmatrix}−\begin{pmatrix}{{a}\:\:\:\:\:{b}}\\{{c}\:\:\:\:\:\:{d}}\end{pmatrix}\:\right]\:=\:\begin{pmatrix}{\mathrm{3}\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\mathrm{3}}\end{pmatrix} \\ $$$$\begin{pmatrix}{{a}\:\:\:\:{b}}\\{{c}\:\:\:\:{d}}\end{pmatrix}\:\begin{pmatrix}{−\mathrm{4}−{a}\:\:\:\:\:\:\:\:−\:{b}}\\{\:\:\:\:\:\:−{c}\:\:\:\:\:\:−\mathrm{4}−{d}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{3}\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\mathrm{3}}\end{pmatrix} \\ $$$$\begin{pmatrix}{−{a}^{\mathrm{2}} −\mathrm{4}{a}−{bc}\:\:\:\:\:\:\:\:−{ab}−\mathrm{4}{b}−{bd}}\\{−{ac}−\mathrm{4}{c}−{cd}\:\:\:\:\:\:\:\:−{bc}−\mathrm{4}{d}−{d}^{\mathrm{2}} }\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{3}\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\mathrm{3}}\end{pmatrix} \\ $$$$\left(\bullet\right)\:−{ab}−\mathrm{4}{b}−{bd}=\mathrm{0}\:;\:{b}\left({a}+\mathrm{4}+{d}\right)=\mathrm{0}\:\rightarrow\begin{cases}{{b}=\mathrm{0}}\\{{a}+{d}=−\mathrm{4}}\end{cases} \\ $$$$\left(\bullet\bullet\right)−{ac}−\mathrm{4}{c}−{cd}=\mathrm{0}\:;\:{c}\left({a}+{d}+\mathrm{4}\right)=\mathrm{0}\rightarrow\begin{cases}{{c}=\mathrm{0}}\\{{a}+{d}=−\mathrm{4}}\end{cases} \\ $$$${for}\:{b}=\mathrm{0}\:\Rightarrow−{a}^{\mathrm{2}} −\mathrm{4}{a}=\mathrm{3}\:;\:{a}^{\mathrm{2}} +\mathrm{4}{a}+\mathrm{3}=\mathrm{0} \\ $$$$\:\left({a}+\mathrm{1}\right)\left({a}+\mathrm{3}\right)=\mathrm{0}\rightarrow\begin{cases}{{a}=−\mathrm{1}\:\wedge{d}=−\mathrm{3}}\\{{a}=−\mathrm{3}\:\wedge{d}=−\mathrm{1}}\end{cases} \\ $$$${A}=\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\:\mathrm{0}\:\:\:\:\:\:−\mathrm{3}}\end{pmatrix}\:{or}\:{A}=\begin{pmatrix}{−\mathrm{3}\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:\:−\mathrm{1}}\end{pmatrix} \\ $$
Commented by liberty last updated on 13/Dec/20
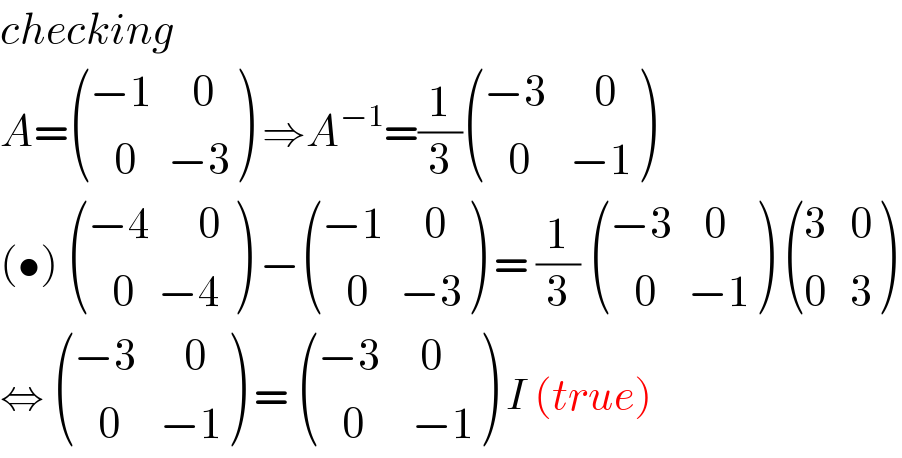
$${checking} \\ $$$${A}=\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:−\mathrm{3}}\end{pmatrix}\:\Rightarrow{A}^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{−\mathrm{3}\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:\:−\mathrm{1}}\end{pmatrix} \\ $$$$\left(\bullet\right)\:\begin{pmatrix}{−\mathrm{4}\:\:\:\:\:\:\mathrm{0}\:}\\{\:\:\:\mathrm{0}\:\:\:−\mathrm{4}}\end{pmatrix}\:−\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:−\mathrm{3}}\end{pmatrix}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\begin{pmatrix}{−\mathrm{3}\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:−\mathrm{1}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{3}\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\mathrm{3}}\end{pmatrix} \\ $$$$\Leftrightarrow\:\begin{pmatrix}{−\mathrm{3}\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:\:−\mathrm{1}}\end{pmatrix}\:=\:\begin{pmatrix}{−\mathrm{3}\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:\:\:−\mathrm{1}}\end{pmatrix}\:{I}\:\left({true}\right) \\ $$
