Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 6739 by Tawakalitu. last updated on 20/Jul/16

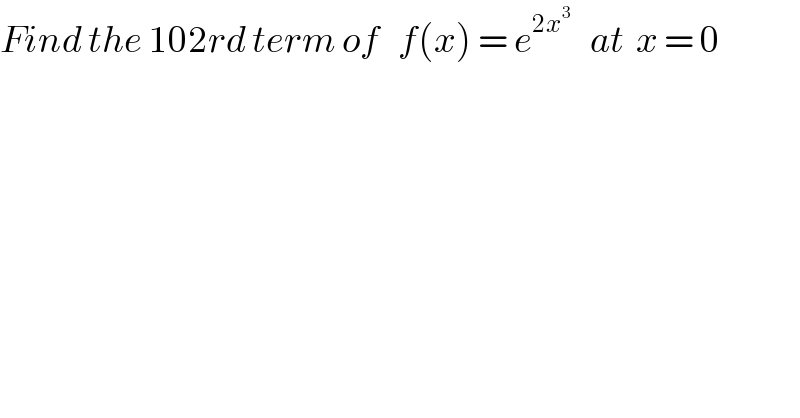
Find the 102rd term of f(x) = e^(2x^3 ) at x = 0

$${Find}\:{the}\:\mathrm{102}{rd}\:{term}\:{of}\:\:\:{f}\left({x}\right)\:=\:{e}^{\mathrm{2}{x}^{\mathrm{3}} } \:\:\:{at}\:\:{x}\:=\:\mathrm{0} \\ $$

Answered by Yozzii last updated on 20/Jul/16

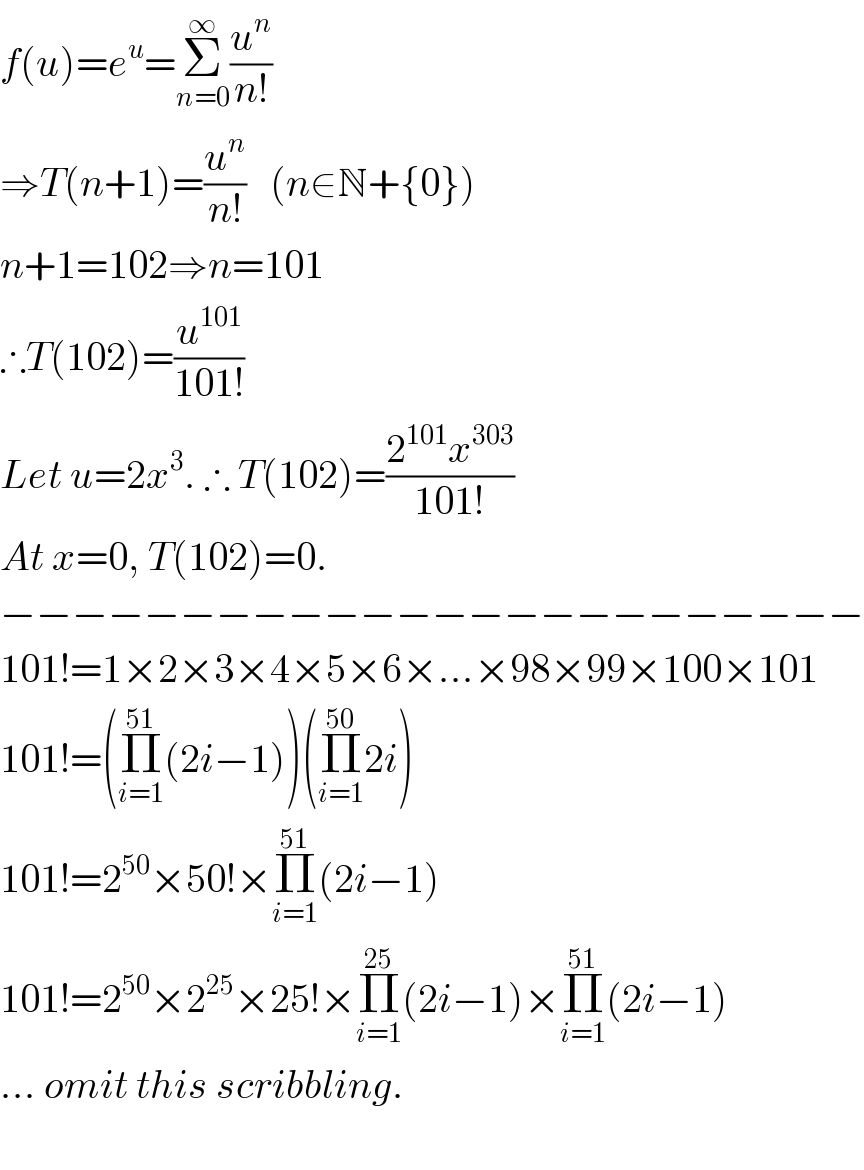
f(u)=e^u =Σ_(n=0) ^∞ (u^n /(n!)) ⇒T(n+1)=(u^n /(n!)) (n∈N+{0}) n+1=102⇒n=101 ∴T(102)=(u^(101) /(101!)) Let u=2x^3 . ∴ T(102)=((2^(101) x^(303) )/(101!)) At x=0, T(102)=0. −−−−−−−−−−−−−−−−−−−−−−−− 101!=1×2×3×4×5×6×...×98×99×100×101 101!=(Π_(i=1) ^(51) (2i−1))(Π_(i=1) ^(50) 2i) 101!=2^(50) ×50!×Π_(i=1) ^(51) (2i−1) 101!=2^(50) ×2^(25) ×25!×Π_(i=1) ^(25) (2i−1)×Π_(i=1) ^(51) (2i−1) ... omit this scribbling.

$${f}\left({u}\right)={e}^{{u}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{u}^{{n}} }{{n}!} \\ $$$$\Rightarrow{T}\left({n}+\mathrm{1}\right)=\frac{{u}^{{n}} }{{n}!}\:\:\:\left({n}\in\mathbb{N}+\left\{\mathrm{0}\right\}\right) \\ $$$${n}+\mathrm{1}=\mathrm{102}\Rightarrow{n}=\mathrm{101} \\ $$$$\therefore{T}\left(\mathrm{102}\right)=\frac{{u}^{\mathrm{101}} }{\mathrm{101}!} \\ $$$${Let}\:{u}=\mathrm{2}{x}^{\mathrm{3}} .\:\therefore\:{T}\left(\mathrm{102}\right)=\frac{\mathrm{2}^{\mathrm{101}} {x}^{\mathrm{303}} }{\mathrm{101}!} \\ $$$${At}\:{x}=\mathrm{0},\:{T}\left(\mathrm{102}\right)=\mathrm{0}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$$\mathrm{101}!=\mathrm{1}×\mathrm{2}×\mathrm{3}×\mathrm{4}×\mathrm{5}×\mathrm{6}×...×\mathrm{98}×\mathrm{99}×\mathrm{100}×\mathrm{101} \\ $$$$\mathrm{101}!=\left(\underset{{i}=\mathrm{1}} {\overset{\mathrm{51}} {\prod}}\left(\mathrm{2}{i}−\mathrm{1}\right)\right)\left(\underset{{i}=\mathrm{1}} {\overset{\mathrm{50}} {\prod}}\mathrm{2}{i}\right) \\ $$$$\mathrm{101}!=\mathrm{2}^{\mathrm{50}} ×\mathrm{50}!×\underset{{i}=\mathrm{1}} {\overset{\mathrm{51}} {\prod}}\left(\mathrm{2}{i}−\mathrm{1}\right) \\ $$$$\mathrm{101}!=\mathrm{2}^{\mathrm{50}} ×\mathrm{2}^{\mathrm{25}} ×\mathrm{25}!×\underset{{i}=\mathrm{1}} {\overset{\mathrm{25}} {\prod}}\left(\mathrm{2}{i}−\mathrm{1}\right)×\underset{{i}=\mathrm{1}} {\overset{\mathrm{51}} {\prod}}\left(\mathrm{2}{i}−\mathrm{1}\right) \\ $$$$...\:{omit}\:{this}\:{scribbling}. \\ $$$$ \\ $$

Commented by Tawakalitu. last updated on 20/Jul/16

Thanks so much

$${Thanks}\:{so}\:{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com