Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 38395 by NECx last updated on 25/Jun/18

Find roots of the equation z^2 +2(1+i)z +2=0 leaving your answer in a+ib

$${Find}\:{roots}\:{of}\:{the}\:{equation} \\ $$$${z}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}+{i}\right){z}\:+\mathrm{2}=\mathrm{0} \\ $$$${leaving}\:{your}\:{answer}\:{in}\:{a}+{ib} \\ $$

Commented by maxmathsup by imad last updated on 25/Jun/18

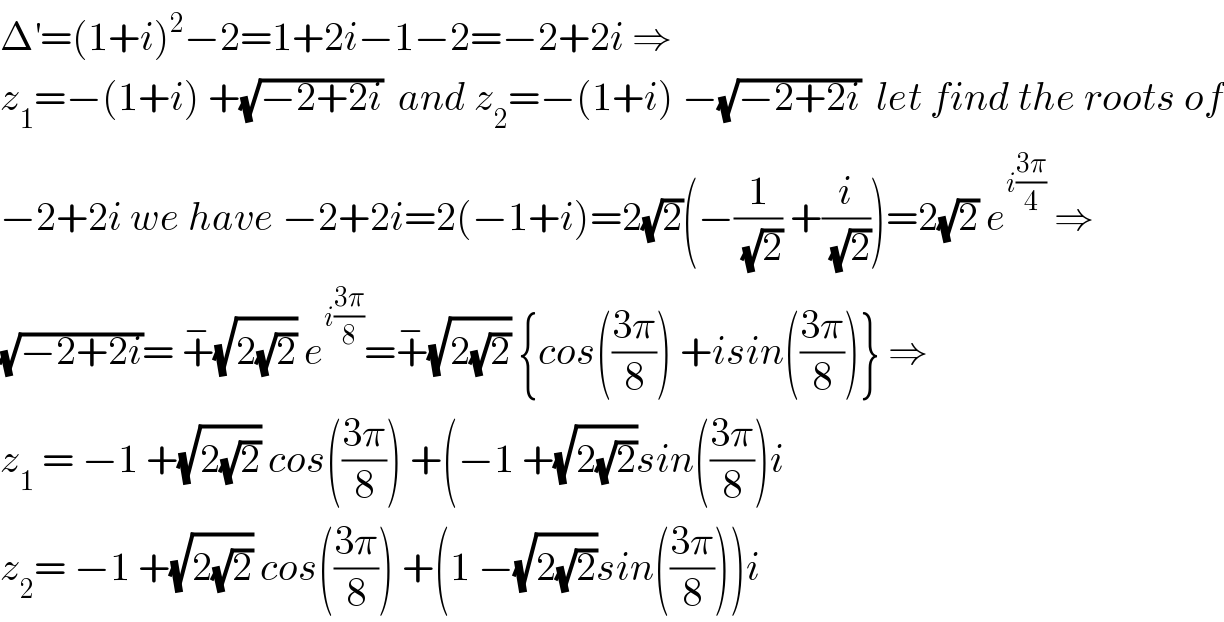
Δ^′ =(1+i)^2 −2=1+2i−1−2=−2+2i ⇒ z_1 =−(1+i) +(√(−2+2i)) and z_2 =−(1+i) −(√(−2+2i)) let find the roots of −2+2i we have −2+2i=2(−1+i)=2(√2)(−(1/(√2)) +(i/(√2)))=2(√2) e^(i((3π)/4)) ⇒ (√(−2+2i))= +^− (√(2(√2))) e^(i((3π)/8)) =+^− (√(2(√2))) {cos(((3π)/8)) +isin(((3π)/8))} ⇒ z_1 = −1 +(√(2(√2))) cos(((3π)/8)) +(−1 +(√(2(√2)))sin(((3π)/8))i z_2 = −1 +(√(2(√2))) cos(((3π)/8)) +(1 −(√(2(√2)))sin(((3π)/8)))i

$$\Delta^{'} =\left(\mathrm{1}+{i}\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{1}+\mathrm{2}{i}−\mathrm{1}−\mathrm{2}=−\mathrm{2}+\mathrm{2}{i}\:\Rightarrow \\ $$$${z}_{\mathrm{1}} =−\left(\mathrm{1}+{i}\right)\:+\sqrt{−\mathrm{2}+\mathrm{2}{i}}\:\:{and}\:{z}_{\mathrm{2}} =−\left(\mathrm{1}+{i}\right)\:−\sqrt{−\mathrm{2}+\mathrm{2}{i}}\:\:{let}\:{find}\:{the}\:{roots}\:{of} \\ $$$$−\mathrm{2}+\mathrm{2}{i}\:{we}\:{have}\:−\mathrm{2}+\mathrm{2}{i}=\mathrm{2}\left(−\mathrm{1}+{i}\right)=\mathrm{2}\sqrt{\mathrm{2}}\left(−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:+\frac{{i}}{\sqrt{\mathrm{2}}}\right)=\mathrm{2}\sqrt{\mathrm{2}}\:{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} \:\Rightarrow \\ $$$$\sqrt{−\mathrm{2}+\mathrm{2}{i}}=\:\overset{−} {+}\sqrt{\mathrm{2}\sqrt{\mathrm{2}}}\:{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{8}}} =\overset{−} {+}\sqrt{\mathrm{2}\sqrt{\mathrm{2}}}\:\left\{{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:+{isin}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\right\}\:\Rightarrow \\ $$$${z}_{\mathrm{1}} \:=\:−\mathrm{1}\:+\sqrt{\mathrm{2}\sqrt{\mathrm{2}}}\:{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:+\left(−\mathrm{1}\:+\sqrt{\mathrm{2}\sqrt{\mathrm{2}}}{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right){i}\right. \\ $$$${z}_{\mathrm{2}} =\:−\mathrm{1}\:+\sqrt{\mathrm{2}\sqrt{\mathrm{2}}}\:{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:+\left(\mathrm{1}\:−\sqrt{\mathrm{2}\sqrt{\mathrm{2}}}{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\right){i} \\ $$

Answered by ajfour last updated on 25/Jun/18

let z=x+iy ⇒ x^2 −y^2 +2ixy+2(1+i)(x+iy)+2=0 x^2 −y^2 +2ixy+2x+2iy+2ix−2y+2=0 _________________________ ⇒ x^2 −y^2 +2x−2y+2=0 and xy+x+y=0 _________________________ ⇒ y= −(x/(1+x)) x^2 −(x^2 /((1+x)^2 ))+2x+((2x)/(1+x))+2=0 x^2 (1+x)^2 −x^2 +2(1+x)^3 +2x(1+x)=0 x^4 +2x^3 +x^2 −x^2 +2+2x^3 +6x^2 +6x +2x+2x^2 =0 x^4 +4x^3 +8x^2 +8x+2=0 (x^4 +4x^3 +6x^2 +4x+1)+2x^2 +4x+1=0 (x+1)^4 +2x^2 +4x+1=0 (x+1)^4 +2(x+1)^2 −1=0 [(x+1)^2 +1]^2 =2 (x+1)^2 =−1+(√2) x=−1±(√((√2)−1)) y= −(x/(x+1)) = ((1∓(√((√2)−1)))/(±(√((√2)−1)))) = (1/(±(√((√2)−1))))−1 z = −1 ±(√((√2)−1))+i((1/(±(√((√2)−1))))−1) . Two roots (using either + or − at both the places the same sign).

$${let}\:{z}={x}+{iy} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{2}{ixy}+\mathrm{2}\left(\mathrm{1}+{i}\right)\left({x}+{iy}\right)+\mathrm{2}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{2}{ixy}+\mathrm{2}{x}+\mathrm{2}{iy}+\mathrm{2}{ix}−\mathrm{2}{y}+\mathrm{2}=\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\:\:\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{y}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{x}}−\mathrm{2}\boldsymbol{{y}}+\mathrm{2}=\mathrm{0}\:\:{and} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{xy}}+\boldsymbol{{x}}+\boldsymbol{{y}}=\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\:\:\:\:{y}=\:−\frac{{x}}{\mathrm{1}+{x}} \\ $$$${x}^{\mathrm{2}} −\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }+\mathrm{2}{x}+\frac{\mathrm{2}{x}}{\mathrm{1}+{x}}+\mathrm{2}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}+{x}\right)^{\mathrm{3}} +\mathrm{2}{x}\left(\mathrm{1}+{x}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}^{\mathrm{2}} +\mathrm{2}+\mathrm{2}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{6}{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:+\mathrm{2}{x}+\mathrm{2}{x}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{2}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}\right)+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)^{\mathrm{4}} +\mathrm{2}\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\left[\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right]^{\mathrm{2}} =\mathrm{2} \\ $$$$\:\:\:\left({x}+\mathrm{1}\right)^{\mathrm{2}} =−\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$\:\:\:\:\:{x}=−\mathrm{1}\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$\:\:{y}=\:−\frac{{x}}{{x}+\mathrm{1}}\:=\:\frac{\mathrm{1}\mp\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}{\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{1}}{\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}−\mathrm{1} \\ $$$$\:\:\boldsymbol{{z}}\:=\:−\mathrm{1}\:\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}+{i}\left(\frac{\mathrm{1}}{\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}−\mathrm{1}\right)\:. \\ $$$$\:\:\:\:{Two}\:{roots}\:\left({using}\:{either}\:+\:{or}\:−\right. \\ $$$$\left.{at}\:{both}\:{the}\:{places}\:{the}\:{same}\:{sign}\right). \\ $$

Commented by MrW3 last updated on 25/Jun/18

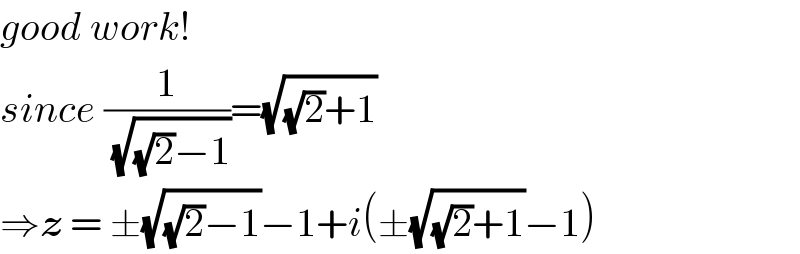
good work! since (1/(√((√2)−1)))=(√((√2)+1)) ⇒z = ±(√((√2)−1))−1+i(±(√((√2)+1))−1)

$${good}\:{work}! \\ $$$${since}\:\frac{\mathrm{1}}{\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}=\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}} \\ $$$$\Rightarrow\boldsymbol{{z}}\:=\:\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}−\mathrm{1}+{i}\left(\pm\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}−\mathrm{1}\right) \\ $$

Commented by malwaan last updated on 25/Jun/18

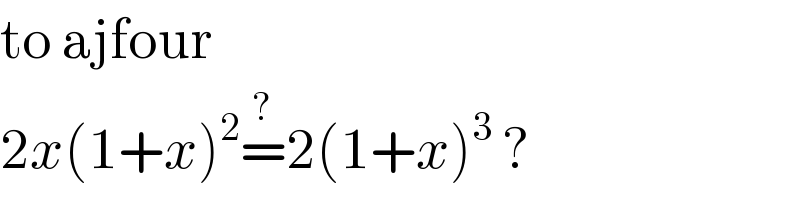
to ajfour 2x(1+x)^2 =^? 2(1+x)^3 ?

$$\mathrm{to}\:\mathrm{ajfour} \\ $$$$\mathrm{2}{x}\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \overset{?} {=}\mathrm{2}\left(\mathrm{1}+{x}\right)^{\mathrm{3}} \:? \\ $$

Commented by ajfour last updated on 25/Jun/18

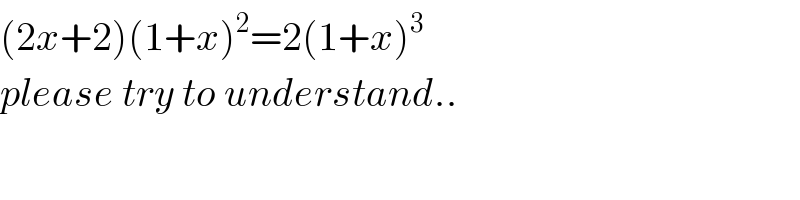
(2x+2)(1+x)^2 =2(1+x)^3 please try to understand..

$$\left(\mathrm{2}{x}+\mathrm{2}\right)\left(\mathrm{1}+{x}\right)^{\mathrm{2}} =\mathrm{2}\left(\mathrm{1}+{x}\right)^{\mathrm{3}} \:\: \\ $$$${please}\:{try}\:{to}\:{understand}.. \\ $$

Commented by malwaan last updated on 25/Jun/18

thank you so much mr ajfour your answer is 100% right thanks Mrw3

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{mr}\:\mathrm{ajfour} \\ $$$$\mathrm{your}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{100\%}\:\mathrm{right} \\ $$$$\mathrm{thanks}\:\mathrm{Mrw3} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com